57584 Str108

212    6. Krzywe eliptyczne

noważno.ści z -l /-ma dokładnie jednego reprezentanta w „podstawowym rów-nolcgłoboku", składającym się z liczb zespolonych postaci aa)_t *f ów₂, gdzie 0 ^ a. h < I (np. jeśli /. jest zbiorem liczb całkowitych Gaussa, to podstawowym równolcgłobokiem jest kwadrat jednostkowy). Ponieważ punkty leżące naprzeciw siebie na równoległych bokach tego równolcgłoboku różnią się o punkt kratowy, są równe w C/L. Myślimy zatem o nich jak o punktach „sklejonych ze sobą". Możemy to sobie wyobrazić w ten sposób, że zwijamy równolcgłobok tak. by jego przeciwległe boki nałożyły się na siebie (tworząc w ten sposób fragment walca), a następnie zwijając w drugą stronę tak, by skleić ze sobą powstałe na końcach walca okręgi; widzimy, że w ten sposób otrzymaliśmy „torus" (obwarzanek), przedstawiony na poniższym rysunku.

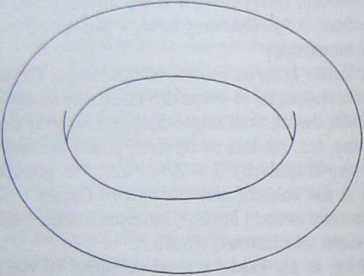
Jako grupa torus jest produktem dwóch okręgów, tzn. jego punkty mogą być opisane parametrycznie przez uporządkowane pary kątów (a, Ę. (Dokładniej, jeśli torus powstał z kraty L = Zco_l + Zu₂, to element grupy ilorazowej C/L można zapisać w postaci aa)_l + bw₂, a następnie wziąć a = Ina, fi = lub). Możemy zatem myśleć o krzywej eliptycznej nad ciałem liczb zespolonych jak o dwuwymiarowym uogólnieniu okręgu na płaszczyźnie rzeczywistej. W rzeczywistości ta analogia sięga dalej, niż moglibyśmy się spodziewać. Otóż „funkcje eliptyczne” (które punktowi (x, y)sE przyporządkowują z powrotem liczbę zespoloną z, dla której (x, y) = (p(z), p'(z))) okazują się mieć pewne własności analogiczne do własności funkcji aresin (która mówi nam, w jaki sposób przejść od punktu na okręgu jednostkowym do liczby rzeczywistej, odpowiadającej temu punktowi, gdy odcinek „nawijamy” na okrąg). Gdy zajmujemy się krzywymi eliptycznymi w algebraicznej teorii liczb, dostrzegamy głębokie analogie między współrzędnymi punktów „podziału na n części” na krzywej eliptycznej (chodzi o punkty P takie, że nP jest punktem O) a punktami podziału okręgu jednostkowego na n części (są to pierwiastki stopnia n z jedności na płaszczyźnie zespolonej). Więcej informacji o tym, jak również o funkcji fp Weicrstrassa (wraz z dowodami jej własności) można znaleźć w książkach wymienionych w bibliografa na końcu tego podrozdziału.

Krzywe eliptyczne nad ciałem liczb wymiernych. Jeśli w równaniu (i) liczby a i b są wymierne, to naturalne jest poszukiwanie rozwiązań wymiernych (x, y). tzn. badanie krzywej eliptycznej nad ciałem Q liczb wymiernych. Teoria krzywych eliptycznych nad ciałem liczb wymiernych jest bardzo rozbudowana. Okazuje się, że grupy abelowe punktów tych krzywych są skończenie generowane (twierdzenie Mordella). Oznacza to, że taka grupa jest produktem skończonej „podgrupy torsyjnej” (punkty skończonego rzędu) oraz podgrupy generowanej przez skończenie wiele punktów nieskończonego rzędu. Liczbę generatorów tej nieskończonej części nazywamy rangą r grupy; jest ona równa zeru wtedy i tylko wtedy, gdy cała grupa jest skończona. Badanie rangi r i innych własności grupy punktów krzywej eliptycznej nad Q jest związane z wieloma interesującymi problemami teorii liczb i geometrii algebraicznej. Na przykład pytanie postawione już w starożytności - „dla jakich liczb n istnieje trójkąt prostokątny, którego boki mają długości wymierne i którego pole wynosi n?” - okazuje się być równoważne pytaniu „czy ranga krzywej eliptycznej y¹ = x² - n²x jest większa od zera?” Przypadek n = 6 i trójkąta 3-4-5 prowadzi do punktu P z przykładu 2, mającego na krzywej y² ~ x³ - 36* rząd nieskończony. Więcej informacji na ten temat znajduje się w książkach cytowanych w bibliografii na końcu tego podrozdziału.

Punkty skończonego rzędu. Rząd N punktu P leżącego na krzywej eliptycznej jest to najmniejsza liczba naturalna taka, że NP = O; oczywiście taka liczba W może nie istnieć. Często ważne jest znalezienie punktów skończonego rzędu na krzywej eliptycznej, zwłaszcza zdefiniowanej nad ciałem Q.

Przykład 3. Wyznaczmy rząd punktu P = (2, 3) na krzywej y¹ = x³ + 1.

Rozwiązanie. Korzystając ze wzorów (5), otrzymujemy 2P = (0,1); korzystając z tych wzorów jeszcze raz otrzymamy 4P = 2(2P) = (0, -I). Zatem 4P = —2P, skąd wynika, że 6P = 0. A więc rząd P jest równy 2,3 lub 6. Ale 2P = (0, 1) ^ O, a gdyby rząd P był równy 3, to mielibyśmy 4P = P, co jednak nie jest prawdą. Zatem punkt P ma rząd 6.

Krzywe eliptyczne nad ciałem skończonym. Do końca tego podrozdziału K będzie ciałem skończonym F_ff mającym q = p^r elementów. Niech E będzie krzywą eliptyczną zdefiniowaną nad ciałem F_fl. Jeśli p = 2 lub p = 3, to krzywa E jest zdefiniowana odpowiednio za pomocą wzorów (2) lub (3) z początku tego podrozdziału.

Łatwo zauważyć, że krzywa eliptyczna E może mieć co najwyżej 2q + 1 F₉-punktów: punkt w nieskończoności oraz 2q par (*, y), przy czym *, yeF,, spełniających równanie (1) (albo (2) lub (3), gdy p = 2 lub p — 3). Mianowicie, dla każdej z q możliwych wartości * istnieją co nawyżej dwie wartości y, które spełniają równanie (1).