69875 Str110

216    6, Krzywe eliptyczne

ru), że (-funkcji! ma szczególną postać. W przypadku krzywej eliptycznej firn Weil udowodnił następujące twierdzenie:    ^ł

Twierdzenie (hipoteza Weila dla krzywej eliptycznej). (■funkcja jest funkcją hy. mierną zmiennej T, określoną następującym wzorem:

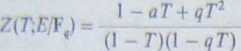
(8)

gdzie tylko liczba całkowita a zależy od krzywej E. Liczba a jest powiązana z liczbą N = wzorem: N = q + 1 - a. Ponadto wyróżnik trójmianu lewad•

rolowego w liczniku jest ujemny (tzn. a² <4q, co wynika z twierdzenia Has-

sego), a więc ten trójmian ma dwa sprzężone pierwiastki zespolone a i fi o module równym q. (Dokładniej rzecz biorąc, pierwiastkami są liczby 1/a i l/p, a nie a i fi.)

Dowód tego twierdzenia znajduje się w § 5.2 książki Silvermana.

Uwaga. Jeśli zapiszemy licznik ułamka we wzorze (8) w postaci (1 — a7)(l - pT), a następnie zróżniczkujemy logarytm obu stron tego wzoru (przy czym lewą stronę zastąpimy definicją (7)), to przekonamy się, że wzór (8) jest równoważny ciągowi następujących zależności:

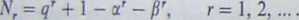
Ponieważ liczba N = N_X wyznacza a, p i o, więc oznacza to, że liczba punktów nad ciałem F₅ wyznacza jednoznacznie liczbę punktów nad dowolnym rozszerzeniem ciała ¥_q. Zatem hipoteza Weila jest, między innymi, przydatna przy wyznaczaniu liczby punktów krzywej nad rozszerzeniem wysokiego stopnia.

Przykład 5. Można łatwo wyznaczyć (-funkcję krzywej eliptycznej o równaniu y² + y = x³ nad ciałem F₂, korzystając z tego, że istnieją tylko trzy F₂-punkty. Jest nią (1 + 2T²)/(1 - T)( 1 - 27), tzn. odwrotnościami pierwiastków licznika są liczby ±ij2 . Prowadzi to do wzoru

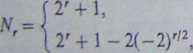
gdy liczba r jest nieparzysta; gdy liczba r jest parzysta.

Na zakończenie tego podrozdziału zauważymy jeszcze, że istnieje wiele analogii między grupą F_q-punktów krzywej eliptycznej i grupą multyplikatyw-ną FJ. Na przykład z twierdzenia Hassego wynika, że mają one w przybliżeniu tę samą liczbę elementów. Jednak konstrukcja grup abelowych punktów krzywej eliptycznej ma zasadniczą przewagę, która decyduje o jej przydatności

w kryptografii: dla ustalonej (dużej) liczby q istnieje wiele różnych krzywych eliptycznych i wiele różnych wartości N do wyboru. Krzywe eliptyczne są bogatym źródłem „naturalnych” skończonych grup abclowych. Skorzystamy

7. tego w następnym podrozdziale.

ćwiczenia

1.    Jeśli £ jest krzywą eliptyczną zdefiniowaną nad ciałem C, której równanie (1) ma współczynniki a, óeR, to punkty krzywej E o współrzędnych rzeczywistych tworzą podgrupę. Jakie możliwe podgrupy grupy punktów krzywej zespolonej E (która jako grupa jest izomorficzna z produktem grupy okręgu ze sobą) są grupami punktów o współrzędnych rzeczywistych? Daj przykład każdej z tych podgrup.

2.    Ile punktów P rzędu n (tzn. takich, że nP = O) istnieje na krzywej eliptycznej zdefiniowanej nad ciałem C? A ile na krzywej zdefiniowanej nad R?

3.    Podaj przykład krzywej eliptycznej nad ciałem R, która ma dokładnie dwa punkty rzędu 2, i inny przykład krzywej, która ma dokładnie cztery punkty rzędu 2.

4.    Niech P będzie punktem na krzywej eliptycznej nad ciałem R. Przypuśćmy, że P nie jest punktem w nieskończoności. Znajdź warunek geometryczny równoważny temu, że P jest punktem rzędu (a) 2; (b) 3; (c) 4.

5.    Każdy z następujących punktów ma skończony rząd na danej krzywej eliptycznej nad Q. W każdym przypadku znajdź rząd P.

(a) P — (0, 16) na krzywej y² = x² + 256.

2’2

(b) P =

* +-r*.

na krzywej y

(c)    P = (3, 8) na krzywej y² = x² — 43* + 166.

(d)    P = (0, 0) na krzywej y² + y = x² - x² (która może być zapisana

* ⁺ 3>‘

w postaci (a) po zamianie zmiennych y -> y —

6.    Wyprowadź wzory na dodawanie punktów, analogiczne do wzorów (4)-(5), dla krzywej eliptycznej nad ciałem charakterystyki 2 oraz 3 (por. równania (2)-(3)).

7.    Udowodnij, że istnieje q +1 F_q-punktów na krzywej eliptycznej o równaniu

(a)    y² = x² — x, gdy q = 3 (mod 4);

(b)    y² = x² — 1, gdy q = 2 (mod 3) i q jest liczbą nieparzystą;

(c)    y² 4- y = *³, gdy q = 2 (mod 3) (q może być liczbą parzystą).

8.    Dla wszystkich potęg q = p^r nieparzystych liczb pierwszych, aż do q — 27, znajdź rząd i typ grupy F.-punktów krzywych eliptycznych y² = x² — * i y^z = x² — 1 (w drugim przypadku dla p # 3). W niektórych przypadkach trzeba będzie sprawdzić, ile punktów ma rząd 3 lub 4.

9.    Niech q — 2^r i niech krzywa eliptyczna E nad ciałem F_fl ma równanie