67722 Transport3

61.' Obliczenie kól pędnych¹)

Ramiona i wieniec kół pędnych przenoszą obciążenia wynikające z momentu skręcającego na wale, z naciągu liny opasującej koło i z nacisku szczęk hamulcowych. Przechodząc kolejno te trzy obciążenia można przyjąć, że moment skręcający od wału koła rozkłada się równomiernie na wszystkie ramiona, które pracują utwierdzone w piaście i w wieńcu koła. Pod wpływem obciążenia wynikłego z momentu skręcającego ramiona odkształcają się .w sposób ipodany na rys. 285 a, gdzie kierunki sił P odniesione' są do oddziaływania ramion, a kierunki M,„ oraz M_p do oddziaływania piasty i wieńca na ramiona.

61.' Obliczenie kól pędnych¹)

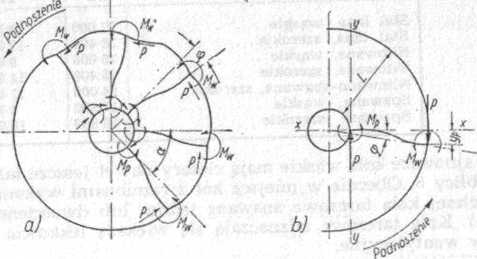
Rys. 285. Odkształcenie kola pędnego pod wpływem momentu skręcającego

a — ugięcie wieńca i ramion, l> — ugięcie ramienia

Równowaga momentów wynikających z sił P działających na obu końcach ramienia i momentów utwierdzenia określa moment w dowolnym punkcie ramienia odległym od piasty o wielkość x

(116)

M_x = M„ — P x

Ponieważ równanie linii ugięcia ma postać EI_ry" = t M_x

więc

EI_ry" — P x — —M_p

skąd

EI_ry'--— = - M_px - Cj

Ponieważ dla x — 0, y — 0 oraz y — 0 więc Ci — 0 a zatem

EI_ry' - ~^Py~ +    = 0

i dalej

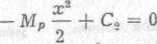
b Obliczenia kól tarczowych, patrz Dodatek.

a ponieważ w myśl powyższych warunków końcowych Co = 0 więc

^M?^x'- _{= 0}

Px³

EI,y —

6 2

ale zarazem dla punktu utwierdzenia w wieńcu na promieniu R, pomijając mały błąd wynikający z odkształcenia wieńca

y_P = <P R — y'_P R

gdzie y' obliczone poprzednio wynosi

^V'"~    El r ('

^PLi--_MpL)

a więc

y»

El, \ 2    /

Wstawiając tę wartość oraz x = L do równania (117) otrzymuje się

„„ PL 3 R-L

Mn = - ' -

3    2R- L

wyzyskując równanie (116), jest

M,„ =

PL 3 R - 2 L

2R

Stąd wynika, że bezwzględna wartość M_p jest zawsze większa od M,_K, a ponieważ obie wartości wypadły dodatnie, więc kierunki działania momentów ,są zgodne z oznaczonymi na rys. 285.

Największy moment zginający w ramionach wynikający z momentu skręcającego wał jest w końcu ramienia po stronie piasty. Siłę P można wyliczyć z warunków równowagi, znając całkowity moment skręcający M, który musi być równy

M = i (PR — M„.)    (113)

skąd

M + i M„

P =

oraz

M_P =

Mp,—

ML 2 i ML 2 i

tU 3 R

3 R- - 3 RL + L-

_3 R — 2 L

3 R² - 3 RL + L²

(119)

(120)

Powyższe dwa równania pozwalają na obliczenie momentów zginających ramion, jeśli znany jest całkowity moment M. W równie prosty sposób .można wyznaczyć momenty gnące wieńca wynikające z momentu skręcającego wał.

Jeśli wytnie się z wieńca wycinek przez środki dwu ramion, to w miejscu przecięcia w środku ramienia działa połowa momentu M_u. i połowa

siły P dając razem w tym miejiscu moment ^RP- . Na przekrój odchylony od ramienia pod kątem <p działa ponadto w przeciwną stronę ta

223