72842 P1080233

4. Wprowadzenie do kinematyki robotów

wtedy

4. Wprowadzenie do kinematyki robotów

c

" = 1 4

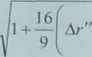
2

a"—a"^{1 2 3} — 1

(4.71)

Przed rozważaniem iteracyjnego rozwiązania zadania prostego manipulatora ą_f przekształca się w a® (rozwiązanie z pierwszego prawidłowo aproksy-mującego równania (4.65)) oraz wyrażenia aj, takiego że

(4.72)

(4.73)

a i = af + af

Otrzymuje się wtedy

^a\ “    2)

^ai =y(#-#)

a\ =~(^2-bl)

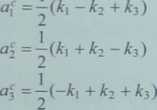
(4.74)

gdzie k otrzymuje się z równania (4.74) dla a\ + a], w którym i,j są brane w porządku cyklicznym

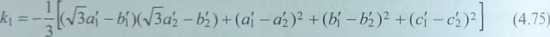
Iterację prowadzi się w następujący sposób:

1) korzystając z równań (4.67) oraz (4.68), zwiększa się rozwinięcie b"

4.4. Kinematyka robotów mobilnych

Ograniczeniami nakładanymi na ruch robota mobilnego są ograniczenia dotyczące przestrzeni, w której może się on poruszać. Nie można przejechać przez ścianę, ani wbić się w podłogę. Opis kinematyki robotów mobilnych ma swoją specyfikę, zależną od ograniczeń ruchu, jakim podlegają roboty, co jest nazywane holono-micznością. Występuje także przeciwstawne pojęcie nieholonomiczności.

W wielu przypadkach robot ze względu na swoją konfigurację ma narzucone pewne więzy. Ograniczenia takie dotyczą robotów holonomicznych. Narzucenie na układ więzów powoduje, że wartości, jakie mogą przyjmować zmienne konfiguracyjne i ich pochodne, podlegają ograniczeniom. Więzy można podzielić na kilka kategorii.

Jeżeli równanie więzów ma postać

F(q,f) = 0    (4.76)

gdzie: F - dowolna funkcja gładka z niezerowaną pierwszą pochodną q — zmienna konfiguracyjną t — czas, są one nazywane geometrycznymi więzami dwustronnymi. Łatwo zauważyć, że w tym przypadku można wyeliminować jedną ze zmiennych konfiguracyjnych, co powoduje zmniejszenie wymiaru przestrzeni konfiguracyjnej.

JeżeU równanie więzów ma postać [98]

F(q,i)< 0 lub F(q, t) < 0    (4.77)

są to geometryczne więzy jednostronne. Typowym przykładem takiego ograniczenia są przeszkody lub mechaniczne ograniczenia zakresu mchów. Takie ograniczenie nie zmniejsza wymiaru przestrzeni konfiguracyjnej, a jedynie definiuje pewien jej podzbiór. Więzy opisane równaniami (4.76) i (4.77) nazywa się holonomicznymi. Holonomiczność oznacza więc, że ograniczenia prędkościowe mchu robota są usuwalne. Robot jest więc holonomiczny, jeśli może zmienić kierunek swojego ruchu (swoją orientację) w miejscu. Roboty takie zwykle rozpatruje się jako punkty materialne poruszające się w przestrzeni, powiększone

0    promień okręgu opisanego na robocie.

Jeżeli równanie więzów ma postać

G(<m,/) = 0    (4.78)

1    równanie to jest niecałkowalne, czyli nie da się go przedstawić w postaci (4.58), to są to nieholonomiczne więzy dwustronne. Więzy takie zmniejszają o jeden wymiar przestrzeń prędkości osiągalnej w danej konfiguracji q, nie ograniczają natomiast przestrzeni konfiguracyjnej.

Jeżeli równanie więzów ma postać [98]

G(#»(M)<0 lub G(q, q, /)<0    (4.79)

i nie da się ich przedstawić w postaci (4.77), to takie więzy są nazywane nieho-^onomicznymi jednostronnym i.    113

1

   z równań (4.72) rozwija się zerowe przybliżenie dla

2

   rozwijane jest d( za pomocą równania (4.71);

3

   korzystając z równań (4.72), znajduje się kolejne przybliżenie a,.

Kroki 3 i 4 powtarza się aż do uzyskania żądanej dokładności określenia

położenia platformy roboczej.

Zadanie odwrotne w przypadku manipulatora typu hexapod jest bardzo łatwe. Rozwiązanie polega na znalezieniu odległości między odpowiednimi przegubami struktury.