89504 PICT5520

264 14. HUmrWY W UKŁADACH WIELOFAZOWYCH

Yilmaz opisał przebieg „* - Ć(Rej w zakresie Re« < 3* I0⁵ Jednym równaniem

- jaws^SL + o.49

^v Rfi4 >/Rc*    1+3I0-*RcJ-*

Współczynnik oporu dla cząstek niekulistych zależy od ich geometrii oraz ukierunkowania podczas ruchu, które może być zmienne w czasie. Fluktuacje te, różne nawet dla cząstek o jednakowej geometrii, zależą od stosunku gęstości cząstek do gęstości cieczy, a dla płynów będących w ruchu także od ich turbulencji. Przykładowe wartości współczynnika oporu w obszarze Newtona dla cząstek o regularnych kształtach przedstawiono w tabł. 14.1 [I]. Są one wyraźnie większe od wartości współczynnika oporu dla cząstek kulistych.

TABLICA 14.1. Wartości współczynnika oporo dla obmni Newtona

1 Kuiah cząstki	<
1 Prostokątna płytka poruszająca się w kierunku prostopadłym do jej rzutu
1 długość	1.2 1.3
j szerokość 1 Walec poruszający się w kierunku równoległym do jego osi	1.9
I dkifość t 1 średnica	0.9
1 Walec poruaząjący się w kierunku prostopadłym do jego osi	0.6
I długość 5	0,6
1 średnica 20	0.9
1	1.2

W literaturze można znaleźć dane dla cząstek nieregularnych, które są jednak obarczone stosunkowo dużym błędem. Istniejące równania uzależniają wartość ( od Re* oraz od sferyczn ości cząstki y. Przykładowo dla zakresu lam i nar-nego współczynnik oporu opisuje równanie [2]

28,46

* “ Re.lg(*/0.065)

W technice procesowej występuje zazwyczaj gromadny ruch cząstek. Opływanie cząstek położonych blisko siebie różni się od opływania cząstki pojedynczej. Dlatego też współczynniki oporów dla tych przypadków są różne. Można ogólnie stwierdzić, że współczynniki oporów podczas ruchu gromadnego są większe aniżeli dla ruchu cząstki pojedynczej.

Dla gromady cząstek monodyspersyjnych w literaturze są podane równania do obliczania współczynnika oporu, z których w praktyce najlepiej sprawdza się

_|4,2. UKŁAD OAZ-CIECZ ^^^^mpiryCTi^Rłchsi-dfOłia i Żaki dla najczęściej występującego przypadku,

_gtj/ie £4 - ułamek objętościowy fazy ciągłej.

Dla liczb Re_d > 0,2 wzajemne oddziaływanie cząstek na siebie jest słabsze,

Stosując równanie (14.18) również dla Re_d > 0.2, stwarza się pewną rezerwę w projektowanym aparacie, tym bardziej że dokładne wyznaczenie wartości _£# jest trudne ze względu na istniejący w aparacie rozkład stężenia cząstek.

Dla układu ciccz-ciecz wyznaczenie współczynnika oporu jest bardziej złożone. W czasie przepływu kropli przez fazę ciągłą zachodzą dodatkowe zjawiska, takie jak cyrkulacja cieczy wewnątrz kropli, deformacja kształtu oraz oscylacja kształtu kropli. Powodują one wystąpienie istotnych różnic między zachowaniem się kropli a zachowaniem się kuli sztywnej i oddziałują na wartość współczynnika oporu przepływu.

Dla liczb Re_d < I kroplę można traktować jako kulę sztywną. W tym zakresie ruchu obowiązuje równanie Stokesa (14.13). Niemniej dla kropel o średnicach powyżej 1 mm zaleca się wprowadzenie poprawki Rybczyńskicgo-Hadamarda

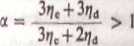
(14.19)

uwzględniającą zwiększoną prędkość kropli cieczy wynikającą z cyrkulacji wewnętrznej [3].

Dla większych wartości liczb Reynoldsa odchylenia kropel od modelowego układu kropli sztywnej są tak duże, że do wyznaczenia ich prędkości stosuje się specjalnie opracowane empiryczne korelacje podane w rozdz. 14.3.

Przy ilościowym wyznaczaniu wartości współczynnika oporu przepływu dla układu pęcherzyki gazu-ciecz Van Kravelen rozróżnia tylko dwa obszary.

Dla obszaru przepływu laminamego, tj. liczb Re_d < 9, wartość współczynnika oporu przepływu jest opisywana równaniem Stokesa (14.13). Dla przepływu turbulcntncgo natomiast, tj. liczb Re_d > 9, współczynnik oporu jest stały

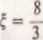
(14.20)

14.2. UKŁAD GAZ-CIECZ

14.2.1. Przepływ wspólprądowy przez rurociągi poziome

W zależności od udziału oraz prędkości poszczególnych faz występują różne rodzaje przepływu mieszaniny cieczy i gazu (rys. 14.3).

Przy bardzo małej zawartości fazy gazowej oraz niedużej jej prędkości faza gazowa jest nieciągła i przepływa w postaci pęcherzy. Jest to przepływ pęcherzy-