Zasady Programowania Strukturalnego (ZAP)
Projekt I - 27.03.07
Dokumentacja projektu
Alicja Zielińska
Grupa 15
Wydział Mechatroniki
Zadanie
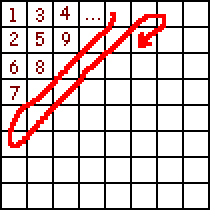
Temat 1
Zapisać w wektorze elementy tablicy kwadratowej w ustalonej kolejności:
Rozwinięcie tematu:
Elementy wektora posortować na parzyste, nieparzyste i zera. Następnie elementy parzyste ustawić w ciąg rosnący a elementy nieparzyste w ciąg malejący.
Dane wejściowe
Danymi wejściowymi są stałe n i m. Stała n określa ilość wierszy/ kolumn w tablicy kwadratowej. Stała m jest kwadratem stałej n i określa wszystkie elementy tablicy/ wektora.
Na podstawie tych dwóch stałych tworzone są dwa typy: tablicowy type Tab=array[1..n,1..n] of integer oraz wektorowy type Wektor=array[1..m] of integer.
Ograniczeniem narzuconym przez Pascala jest to, że typy tablicowy i wektorowy są tworzone na stałych a nie zmiennych dynamicznych czyli są określane z góry (w samym algorytmie) i nie ma możliwości zmiany ich po uruchomieniu programu.
Krótki opis działania programu
Po uruchomieniu program pyta nas w jaki sposób chcemy utworzyć naszą tablicę kwadratową (A). Do wyboru mamy: ręczne wpisywanie wartości, losowanie wartości z podanego przedziału lub numerowanie komórek tablicy po kolei. Wyboru dokonujemy wpisując literkę a, b lub c. Program odczytuje wpisaną wartość jako zmienną ab typu char i, w zależności od jej wartości, wykonuje wybraną przez nas metodę tworzenia tablicy.
Następnie program drukuje tablicę wierszami i, w ten sam sposób co poprzednio, pyta o sposób tworzenia wektora B. Do wyboru mamy przepisywanie wartości: poziomo „wężykiem”, „wężykiem” po głównej przekątnej (co jest głównym zadaniem) oraz ukośnie po drugiej przekątnej. Po wybraniu interesującej nas opcji, program drukuje wektor B i sortuje jego wyrazy w wektorze C.
Podprogramy
Tworzenie tablic
Tablice możemy utworzyć na trzy sposoby:
UT_w - tworzy tablicę poprzez sczytywanie wyrazów wpisanych przez użytkownika;
UT_r - tworzy tablicę z losowymi elementami. Ciekawym urozmaiceniem jest możliwość wyboru zakresu, z którego elementy będą losowane. Odbywa się to przy pomocy zmiennej za;
UT_k - numeruje elementy tablicy w kolejności od 1 do n. Funkcja przydatna przy testowaniu poprawności działania programu;
Drukuj - drukuje tablicę wierszami;
Tworzenie wektorów z elementów tablicy
UW_poz - elementy tablicy przepisywane są wierszami, pierwszy wiersz od początku, drugi od końca i tak na zmianę;
UW - główne zadanie programu
Procedura dzieli się na dwie części - przepisywanie wyrazów znad drugiej głównej przekątnej (włącznie z tą przekątną) i spod niej.
Wyrazy będziemy przepisywać po przekątnych równoległych do głównej przekątnej. Zauważmy, że liczba tych przekątnych wynosi tyle, ile jest kolumn/ wierszy w tablicy (pętla for k:=1 to n do) oraz, że liczba elementów w każdej przekątnej jest równa numerowi kolejności tej przekątnej (pętla for l:=1 to k do). Ponieważ chcemy, aby wyrazy były przepisywane „wężykiem”, dlatego co druga przekątna musi być przepisywana z góry do dołu a co druga z dołu do góry. Służy do tego komenda if k mod 2 = 0 then ... else.
Wyrazy wektora B numerujemy zmienną dynamiczną i, natomiast wyrazy tablicy mają współrzędne [x,y]. Zmienne i oraz x wzrastają o 1 natomiast zmienna y maleje z każdym przepisanym wyrazem. W zależności od tego czy przekątna jest parzysta czy nieparzysta, współrzędne x i y zamieniają się miejscami:
i:=0;
for k:=1 to n do
begin
x:=0; y:=k+1;
for l:=1 to k do
begin
i:=i+1; x:=x+1; y:=y-1;
if k mod 2 = 0 then W[i]:=T[y,x]
else W[i]:=T[x,y];
end
end;
Druga część tej procedury (dla wyrazów spod drugiej głównej przekątnej) jest bardzo podobna do pierwszej jednakże liczba przekątnych zmniejsza się o jedną, liczba wyrazów tychże przekątnych maleje a współrzędne [x,y]dla kolejnych wyrazów wektora zależą od czterech warunków. Ma na to wpływ parzystość zmiennej n:
for k:=2 to n do
begin
x:=k-1; y:=n+1;
for l:=n-k+1 downto 1 do
begin
i:=i+1; x:=x+1; y:=y-1;
if (k mod 2 = 0) and (n mod 2 = 0) then W[i]:=T[x,y];
if (k mod 2 = 0) and (n mod 2 <> 0) then W[i]:=T[y,x];
if (k mod 2 <> 0) and (n mod 2 = 0) then W[i]:=T[y,x];
if (k mod 2 <> 0) and (n mod 2 <> 0) then W[i]:=T[x,y];
end
end;
UW2 - elementy tablicy przepisywane są po przekątnych równoległych do głównej przekątnej od góry do dołu;
DrukujW - drukuje wektor;
Sortowanie
Sortowanie wartości elementów wektora B w wektor C przebiega w dwóch fazach:
parzyste, nieparzyste i zera
Pętla od i=1 do m powoduje sczytanie wszystkich elementów wektora. Na początku sprawdzamy, czy wartość wektora jest różna od zera. Jeśli tak, to sprawdzamy czy jej reszta z dzielenia przez 2 jest równa zero. Jeśli tak, oznacza to, że liczba jest parzysta. Wtedy przepisujemy wartość tego elementu wektora B do kolejnego elementu wektora C oraz zwiększamy ilość liczb parzystych o 1 (zmienna pa - potrzebna w drugiej fazie sortowania). Następnie tworzymy podobną pętlę dla liczb nieparzystych z tą różnicą, że nie zerujemy zmiennej j (która oznacza kolejne wyrazy wektora C) oraz zmieniamy warunek - reszta z dzielenia aktualnej wartości musi być różna od zera. Na koniec pozostałe elementy wektora C wypełniamy zerami i drukujemy.
parzyste rosnąco, nieparzyste malejąco
Dzięki zmiennym pa i np naliczanym w poprzedniej części mamy zakresy sortowania w drugiej fazie. Dla wszystkich elementów parzystych/ nieparzystych sprawdzamy czy wartość aktualnego elementu jest większa/ mniejsza od następnego. Jeżeli jest to dokonujemy ich zamiany. Na koniec pozostałe elementy wypełniamy zerami i drukujemy wektor.
Zestawy danych testowych
n=3; elementy tablicy numerowane po kolei (c); wektor po drugiej przekątnej (c)

n=4; elementy tablicy losowane z przedziału (-6,6) (b); wektor po głównej przekątnej (b)

n=5; elementy tablicy losowane z przedziału (-20,20) (b); wektor poziomo (a)

Wyszukiwarka
Podobne podstrony:
Programowanie strukturalne w C
plikus pl Programowanie strukturalne, Wyklad z C
Bierzmowanie - liturgia, Dokumenty Zasady doboru pieśni, instrukcja Episkopatu i.t.p
Programowanie strukturalne i obiektowe
Programowanie strukturalne i obiektowe Podręcznik do nauki zawodu technik informatyk
Śpiewy podczas nabożeństw, Dokumenty Zasady doboru pieśni, instrukcja Episkopatu i.t.p
Zmienne tablicowe, INFORMATYKA, INFORMATYKA sem. III, 2.Prograowanie strukturalne i obiektowe
Programowanie strukturalne i obiektowe Podrecznik do nauki zawodu technik informatyk prstko
ZASADY PROGRAMOWANIA IMPREZ TURYSTYCZNYCH, TURYSTYKA, podstawy turystyki
BLOKI, Programowanie strukturalne i obiektowe, C ++, Ćwiczenia C++ (skan)
CNC ZASADY PROGRAMOWANIA, CNC
Programowanie opracowanie, Informatyka, Informatyka semestr II, 3.Programowanie strukturalne i obiek
więcej podobnych podstron