100 101

ioo

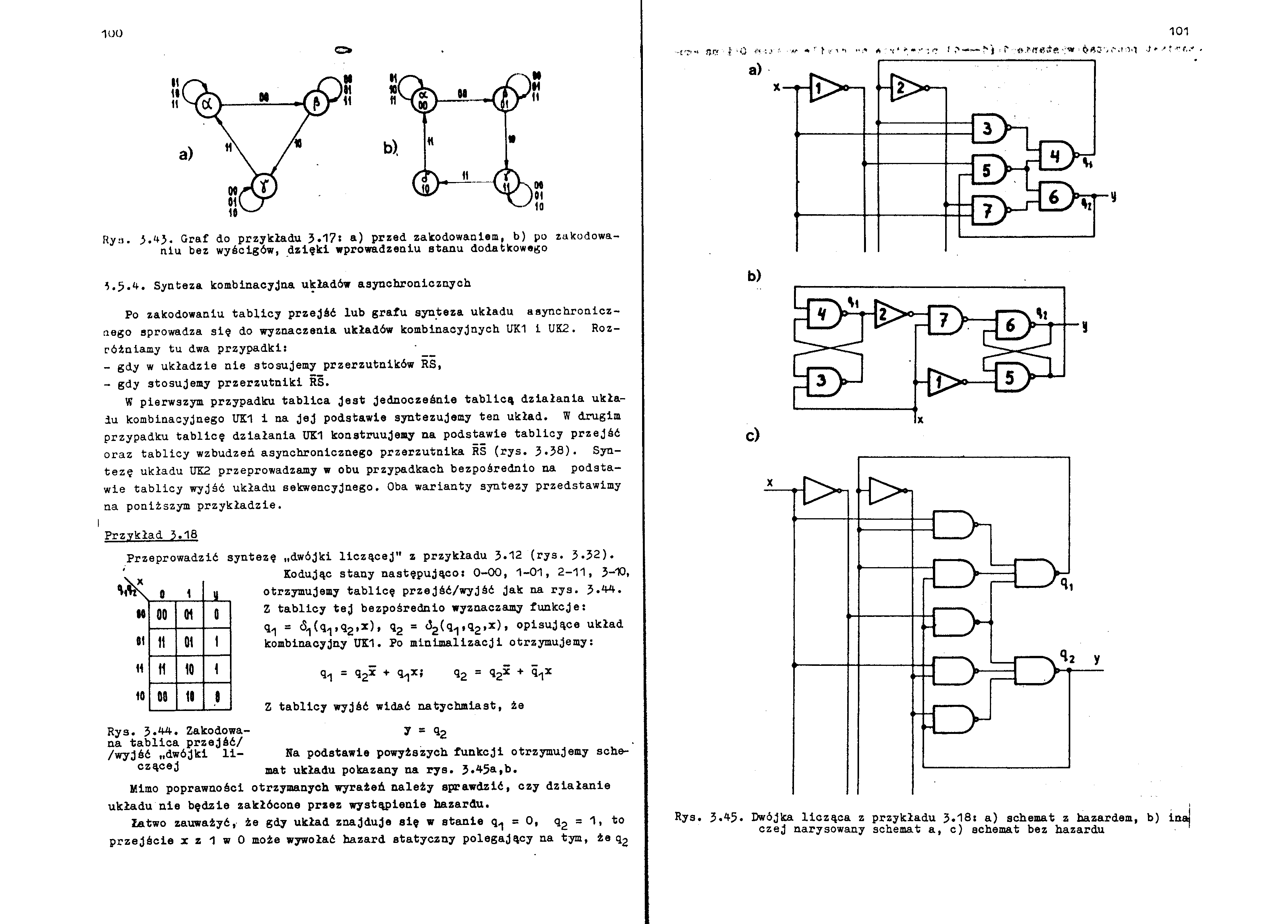
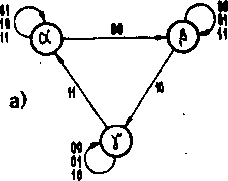
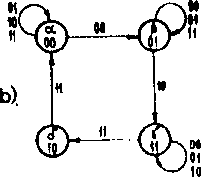
Rya. i.¹*}. Graf do przykładu 3*17* a) przed zakodowaniem, b) po zakodowaniu bez wyścigów, dzięki wprowadzeniu stanu dodatkowego

i.5.*ł-. Synteza kombinacyjna układów asynchronicznych

Po zakodowaniu tablicy przejść lub grafu synteza układu asynchronicznego sprowadza się do wyznaczenia układów kombinacyjnych UK1 1 UK2. Rozróżniamy tu dwa przypadki!

-    gdy w układzie nie stosujemy przerzutników RS,

-    gdy stosujemy przerzutnikl RS.

W pierwszym przypadku tablica Jest Jednocześnie tablicą działania układu kombinacyjnego UK1 i na jej podstawie syntezujemy ten układ. W drugim przypadku tablicę działania UK1 konstruujemy na podstawie tablicy przejść oraz tablicy wzbudzeń asynchronicznego przerzutnlka RS (rys. 3.38). Syntezę układu UK2 przeprowadzamy w obu przypadkach bezpośrednio na podstawie tablicy wyjść układu sekwencyjnego. Oba warianty syntezy przedstawimy na poniższym przykładzie.

I

Przykład 3.18

Przeprowadzić syntezę „dwójki liczącej" z przykładu 3.12 (rys. 3.32).

0	1	II
00	01	0
li	01	1
II	10	1
00	11	0

Kodując stany następująco! 0-00, 1-01, 2-11, 3-10, otrzymujemy tablicę przejść/wyjść Jak na rys. 3.W.

Z tablicy tej bezpośrednio wyznaczamy funkcje: q₁ = <S₁(q₁,q₂iX)« q₂ = <J₂(q₁»q2>^x)> opisujące układ kombinacyjny UK1. Po minimalizacji otrzymujemy:

q₁ = q₂x + q^x; q₂ = q₂x + q,,x Z tablicy wyjść widać natychmiast, że

Rys. 3.W. Zakodowa-    y = q_

na tablica przejść/    *

/wyjść „dwójki li- Ra podstawie powyższych funkcji otrzymujemy sche-^cz^^oe^    mat układu pokazany na rys. 3«^5a,b.

Mimo poprawności otrzymanych wyrażeń należy sprawdzić, czy działanie układu nie będzie zakłócone przez wystąpienie hazardu.

Łatwo zauważyć, że gdy układ znajduje się w stanie q^ = O, q₂ = 1, to przejście x z 1 w O może wywołać hazard statyczny polegający na tym, że q₂

c)

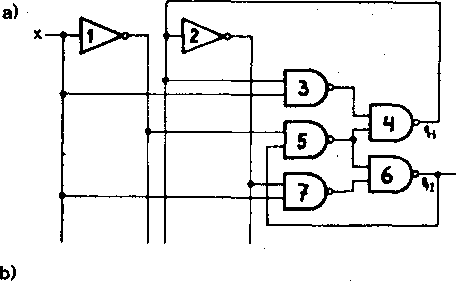
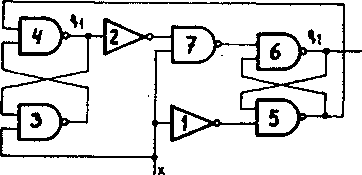
^Rys* 3*45* Dwójka, licząca z przykładu 3*18i a) schemat z hazardem, b) inj czej narysowany schemat a, c) schemat bez hazardu