100 101

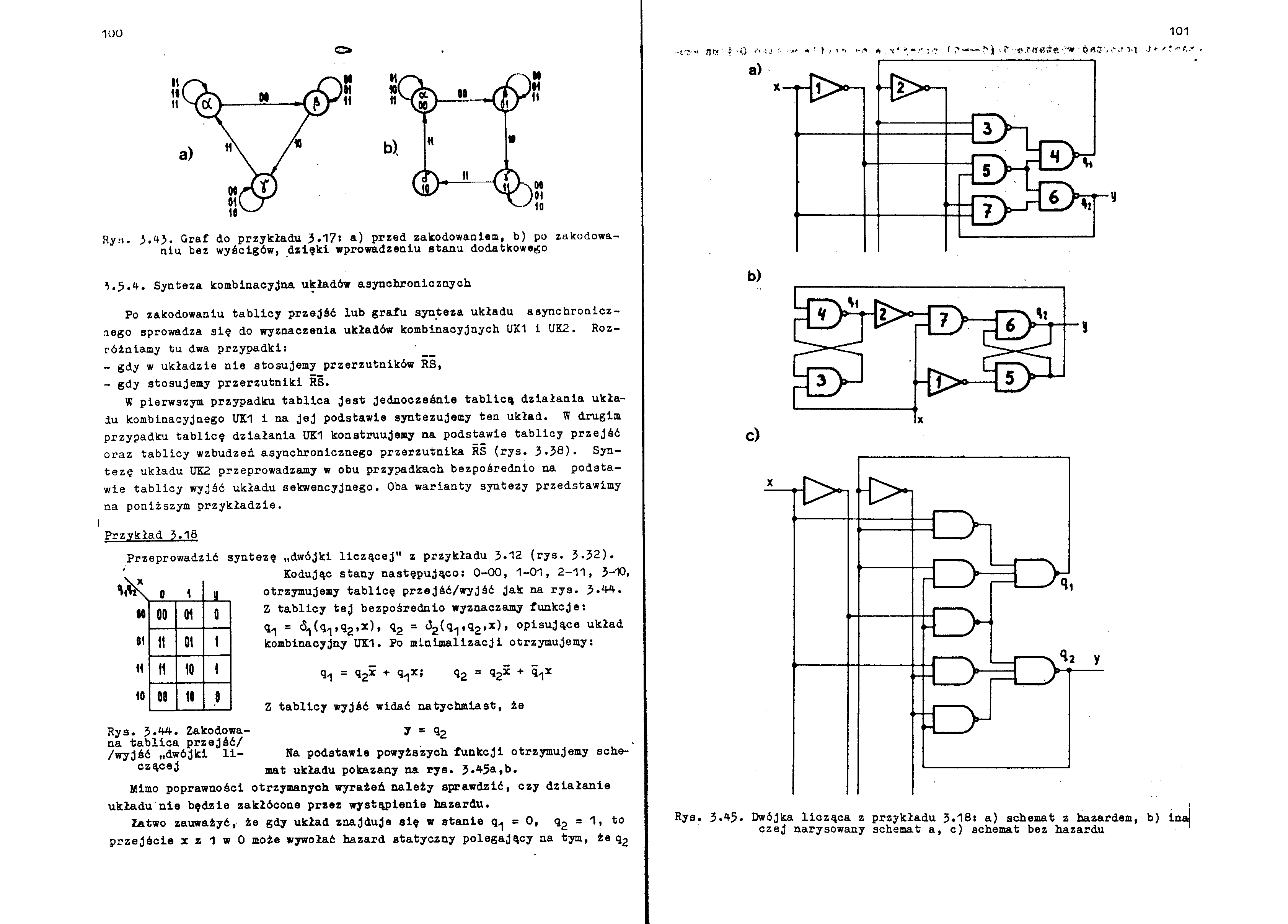
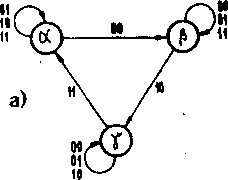
Rya. i.¹*}. Graf do przykładu 3-17* a) przed zakodowaniem, b) po zakodowaniu bez wyścigów, dzięki wprowadzeniu stanu dodatkowego

3.5.ą. Synteza kombinacyjna układów asynchronicznych

Po zakodowaniu tablicy przejść lub grafu synteza układu asynchronicznego sprowadza się do wyznaczenia układów kombinacyjnych UK1 1 UŁ2. Rozróżniamy tu dwa przypadki:

-    gdy w układzie nie stosujemy przerzutników RS,

-    gdy stosujemy przerzutniki RS.

W pierwszym przypadku tablica Jest Jednocześnie tablicą działania układu kombinacyjnego UK1 i na jej podstawie syntezujemy ten układ. W drugim przypadku tablicę działania UK1 konstruujemy na podstawie tablicy przejść oraz tablicy wzbudzeń asynchronicznego przerzutnlka RS (rys. 3.38). Syntezę układu UK2 przeprowadzamy w obu przypadkach bezpośrednio na podstawie tablicy wyjść układu sekwencyjnego. Oba warianty syntezy przedstawimy na poniższym przykładzie.

I

Przykład 3.18

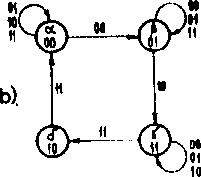
Przeprowadzić syntezę „dwójki liczącej” z przykładu 3.12 (rys. 3.32).

0	1	0
00	01	0
11	01	1
11	10	1
00	10	0

Kodując stany następująco: 0-00, 1-01, 2-11, 3-10, otrzymujemy tablicę przejść/wyjść Jak na rys. 3.W.

Z tablicy tej bezpośrednio wyznaczamy funkcje: q₁ = tS₁(q₁,q₂.3c), q₂ = <S₂(q₁ ,q₂ix), opisujące układ kombinacyjny UK1. Po minimalizacji otrzymujemy:

q₁ = q₂x + q_nx; q₂ = q₂x + q,,x Z tablicy wyjść widać natychmiast, że

Rys. 3.W. Zakodowana tablica przejść/ /wyjść „dwójki liczącej

7 = q₂

Ra podstawie powyższych funkcji otrzymujemy schemat układu pokazany na rys. 3*45a.,b.

Mimo poprawności otrzymanych wyrażeń należy sprawdzić, czy działanie układu nie będzie zakłócone przez wystąpienie hazardu.

Łatwo zauważyć, że gdy układ znajduje się w stanie q^ = 0, q₂ = 1, to przejście x z 1 w 0 może wywołać hazard statyczny polegający na tym, że q₂

-r?*^ł ł-O

-V| > r    --w • o^cr,«-.».•).i •/' ••' r ''*.•*

» ;«, A V *>«• •'

c)

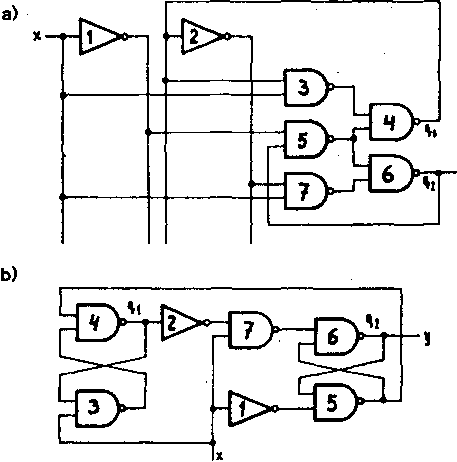
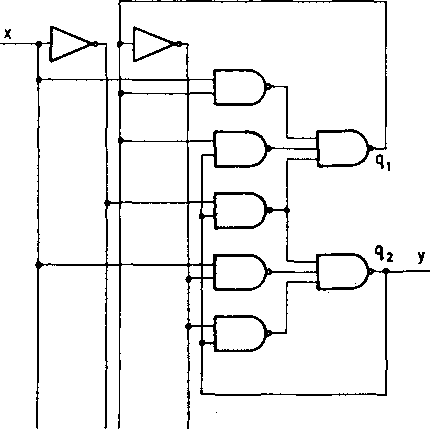
Rys. 3.45. Dwójka licząca z przykładu 3.18* a) schemat z hazardem, b) ind czej narysowany schemat a, c) schemat bez hazardu