12165 ullman122 (2)

-.'V

4 DZIAŁANIA W MODELU RELACYJNYM

Następne przetwarzanie nic powoduje juz powstania żadnych nowych krotek, a zatem przerywamy obliczenia. Właściwy obraz relacji Następny, powstały w wyniku obliczeń /. punktem stałym, jest zawarty na rys. 4.18.

4.4.3. Równania z punktem stałym w Datalogu

Wyrażenia algebry relacji zawierające równania z punktem stałym bywają mocno skomplikowane. Często bywa tak. że równania okazują się prostsze po zapisaniu w postaci zestawu reguł Datalogu i właśnie ten temat zostanie opisany w bieżącym punkcie. Natomiast w podrozdziale 5.10 zostanie przedstawiony sposób implementacji tej koncepcji w SQL3, gdzie notacja z punktem stałym bardziej przypomina zapis algebraiczny niż logiczny, co wynika ze stylu zapisu użytego w SQL3.

Zasadniczy pomysł równań punktu stałego w konwencji logiki polega na rozpoczęciu od jednej lub kilku relacji, których wartości są znane, Mogą to być albo relacje ekstensjonalne bazy danych, albo relacje typu I⁷.DR. Pozostałe relacje definiuje się w nagłówkach reguł. Są to albo intensjonalnc relacje bazy danych. albo relacje typu IDB. Pod/adania w treści reguł zawierają predykaty, które są albo relacjami EDB lub IDB, albo atomami arytmetycznymi. Jeśli któreś relac je IL)B są definiowane w regułach, które w treści też je zawierają, to te reguły są efektywnymi równaniami ze stałym punktem, podobnie jak w przypadku równań algebry relacji w przykładzie 4.34.

PRZYKł Al) 4.36

Następujące dwie reguły Datalogu definiują relację typu 1DR Następny:

Następny (x, y) «— Kolejny(x, y)

Następny (x, y) «— Kolejny(x, z) AND Następny (z, y)

Pierwsza reguła jest podstawowa: mówi ona, że każdy kolejny odcinek jest następnym. Ta reguła odpowiada pierwszemu termowi równania sumy z przykładu 4.34.

W drugiej regule określono, żc każde następstwo kolejnego odcinka x jest również następstwem samego x. Mówiąc ściślej: jeśli r jest kolejnym odcinkiem x, a wiemy, ż.c z następuje po y, to;- następuje również po x.

□

Reguły występujące w przykładzie 4.36 ora/, równanie z punktem stałym w przykładzie 4.35 mają takie same znaczenie, bowiem wartość relacji Następny, jako rozwiązanie równania, jest taka sama jak relacja uzyskana z przetworzenia reguł. W ogólnym przypadku, jeśli żadna z reguł wchodzących w zestaw definiujący pewną relację typu IDB nie zawiera w jakimś po-dzadaniu operatora negacji, to możemy obliczyć tę relację w sposób iteracyj-ny. rozpoczynając od przypisania tej relacji wartości pustej, a następu w kolejnych krokach dołączając do niej nowe wartości wyliczane prze/ sti sowanic reguł do relacji EDB oraz wartości relacji IDB wyliczonej w p< przednim kroku iteracji. Postępowanie iteracyjne kończymy wówczas, gdy n powstają już żadne nowe elementy.

PRZYKŁAD 4.37

Bardziej złożony przykład rekurcncji powstaje w przypadku analizy dro; w gratach Na rysunku 4.19 przedstawiono graf. który reprezentuje pewr rejsy samolotów dwóch hipotetycznych linii lotniczych Nieznana Linia (U/ oraz Typowa Linia (AA), rejsy pomiędzy miastami San Francisco. Dcnvc Dallas, Chicago i Nowym Jorkiem.

AA 1900-2200

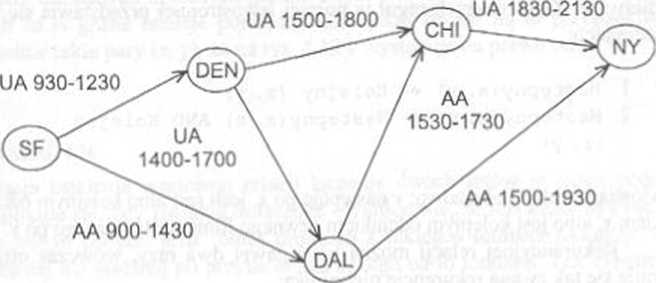
RYSUNEK 4.19

Mapa rejsów niektórych linii lotniczych

Rejsy można zapisywać w następującej relacji typu EDB:

Rejsy i linia, z, do, odlot:, przylot)

Przykładowe krotki z zapisem danych, reprezentowanych w grafie rys. 4.19, umieszczono w tabeli na rys. 4.20.

linia lutnicza		do	odlot	przylot
UA	SF	DEN	930	1230
AA	SF	DAL	900	14 30
UA	DEN	CHI	1500	1800
UA	DEN	DAL	1400	1700
AA	DAL	CHT	1530	1730
AA	DAL	NY	1500	1930
AA	CHI	NY	1900	2200
UA	CHI	NY	1830	2130

RYSUNEK 4.20 Krotki relacji Rejsy