12

Sprawdzian 3

1 Wyznarz asymptotyczne charakterystyki lunplitudowo-łazuwi' Bodego dla obiektu opisanego-tnui&mitanrjit G(*) i ukrwtf, czy obiekt ten po objęciu pętlu jednostkowego ujemnego sprzę/ema zwrotnego będzie stabilny

«(0.1* ♦ 1)(100* I)

^w TrnmnT)

2 W'vkre*l rharakt«ryiitykę NyquisU dla układu opisanego trausmitancją

G’(m)

K$

(^T* + 0

3. Układ o transiuitanijł G{t) yrri]    j*«fa«iUu»wym ujemnym »poi^

żenieni zwrotnym OkrrAł wartości wspólczynuikAw K l r j«Ui wiadomo, ze dla otrzymanego układu maksymalne pr/errguk>wanir wynosi A/_f ■ 0.25 natomiast dwuprocentowy cza* regnbw ji l₇% - Sar k

■I Wyznacz obszar na płaszczyźnie a. w którym |>owinny malm się łucguny układu II rzędu aby spełnione były poniższe wymagania

•    maksymalne jtr/eregultiwanłe 10*/ < Af_r» < 25^f

•    dwuprocentowy etat rcgularji ^ -IseA

5. Ołrtekt o tranwnitancji G(») *» objęto jednostkowym ujonnym sprrę-łankm zwrotnym Wyznarz jaki Ujdzie uchyb w stanic ustalonym, w przypadku |>obud*riiii» uzyskanego układu sygnałem u(<) — łl(ł)

/.ad. I.

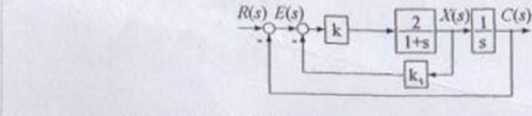
Jakie powinny być wzmocnienia i i zapewniające:

-    stabilność układu zamkniętego

* tłumienie krytyczne (odpowiedź skokowa układu zamkniętego będzie odpowiedzią najszybsza bez pirzcrcgulowania)

-    czas ustalaniu odpowiedzi skokowej l_trs s 0,25j .

Zad. 2.

Wyznaczyć przebieg linii pierwiastkowych zamkniętego układu sterowania z sterownikiem proporcjonalnym i jednostkowym sprzężeniem zwrotnym, dla obiektu o transmitancji

G,(j)

k

Korzystając z kry terium Koutha podaj dla jakiej wartości wzmocnienia k układ zamknięty znajdzie się na granicy stabilności. Dla jakiego wzmocnienia k transmitancja układu zamkniętego charakteryzuje się podwójnym biegunem.

Zad. 3.

Nary suj wykres Nyquista układu opisanego transmitancją

G,(i)

2

Czy po zamknięciu transmitancji G,(s) jednostkowym ujemny m sprzężeniem zwrotnym, układ zamknięty będzie układem stabilnym. Odpowiedź, uzasadnij korzystając z kryterium Nyquisla..