15995 skanuj0061 (10)

B. Cieślar

^ł02_i_<_

II __

^m8x n;(2d)⁴ ‘

32

Funkcje momentów skręcających (rys. 3.3.2)

M| = M-*; Mu = Mi + M2.

Podstawiając powyższe zależności do równania (3) otrzymamy:

₌ M, = 7M, = 350 kNm.

M₁    ^2    1

44—

u    m₂ 1

r—| ■■■ B    C

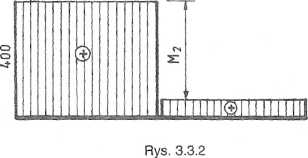
[kNm]

Obciążenie pręta momentem M2 = 350 kNm spowoduje równoczesne osiągnięcie w każdym przekroju pręta 'Ch_Mx. Podobny efekt można uzyskać przykładając moment M₂ = 450 kNm, ale kręcący przeciwnie do założonego na rys. 3.3.1.

Stalowy pręt (rys. 3.4.1) obciążono trzema parami sił Mi, M₂ i Ma. Zapro

jektować z warunku wytrzymałości i sztywności kołowe przekroje poprzeczne pręta zakładając, iż średnica pręta na odcinku AC powinna być półtorakrotnie większa od średnicy pręta na odcinku CD. W obliczeniach przyjąć: Mi = 360 kNm, M₂ = 90 kNm, M3 = 180 kNm, fd = 120 MPa, 9 = 2°, G = 8-10⁴ MPa, I m 0,9 m. Sporządzić wykresy momentów skręcających i kąta skręcenia całkowitego.

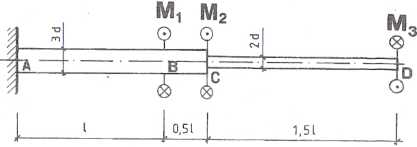
Rys. 3.4.1

Rozwiązanie

Momenty skręcające (rys. 3.4.2a).

M|= -Mi+ M₂ - M₃ = 270 kNm;

Mh= -Mr M₂ = -90 kNm;

Min= -Mi =-180 kNm.

Obliczenie kątów skręcenia całkowitego

<Pa = 0;

= <Pa ^{+ (}Pb,a =

M,l

GJ„

270-10 0,9

8-10

₄ 7c(3d)⁴ 32

= 3,82-10“

M.l

<Pc =9b⁺⁽Pc3=7q-+

^GJoj

M„0,5I

270-10^-3 -0,9 _[ (-90-10~³)0,5-0,9    ₁₀-⁷_1-

₈.₁₀^    ₈.₁₀4iE(3dr    "■    r

32    32

■»=<Pc + <P»,00.,0-, 1 G^J0JB    d Q _1Q4 ”(2d)    d⁴

32

Wykres kąta skręcenia całkowitego pokazano na rys. 3.4.2c.

Projektowanie przekrojów pręta z warunku wytrzymałości:

■^ma* — fd>

Przedział I - średnica pręta di =3d 270-10“³1,5d

rc(3d)⁴

32

<120:

270-10^ -32 _iao.

«07H³    ’

_ / 270 • 10^-3 -16

d>3-;

V JI27-120

d> 0,07515 m.