18816 Obrazek10

Odpowiedzi do arkusza egzaminacyjnego P-9

Odpowiedzi do zadań zamkniętych

Nr zadania	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Odpowiedź	A	D	A	B	C	D	D	B	A	D	C	B	C	C	B
Nr zadania	16	17	18	19	20	21
Odpowiedź	A	C	D	B	B	C

Odpowiedzi i wskazówki do zadań otwartych

Numer zadania	Odpowiedź						Wskazówka
22	2n - 6,28 e NW						Zauważ, że liczba 3,14 - jt jest ujemna.
23	'• \<P\ = 60°, \<Q\ = 80°, |<5| = 40°						Wykorzystaj własność: miary kątów środkowych koła są proporcjonalne do długości łuków, na których są oparte; następnie skorzystaj z twierdzenia o kątach wpisanych i środkowych w kole.
24	1,5						Zauważ, że log22 - 1.
25	ok. 37 cm						Wykorzystaj wzórp = y, gdziep oznacza gęstość, m - masę, a V- objętość danej substancji.
26	xs{-5, -1,0,1}						Przenieś wszystkie wyrazy równania na jedną stronę i rozłóż tę stronę na czynniki.
27	dowód						Wykorzystaj trzy razy wzór na długość promienia okręgu wpisanego w trójkąt prostokątny w zależności od długości boków.
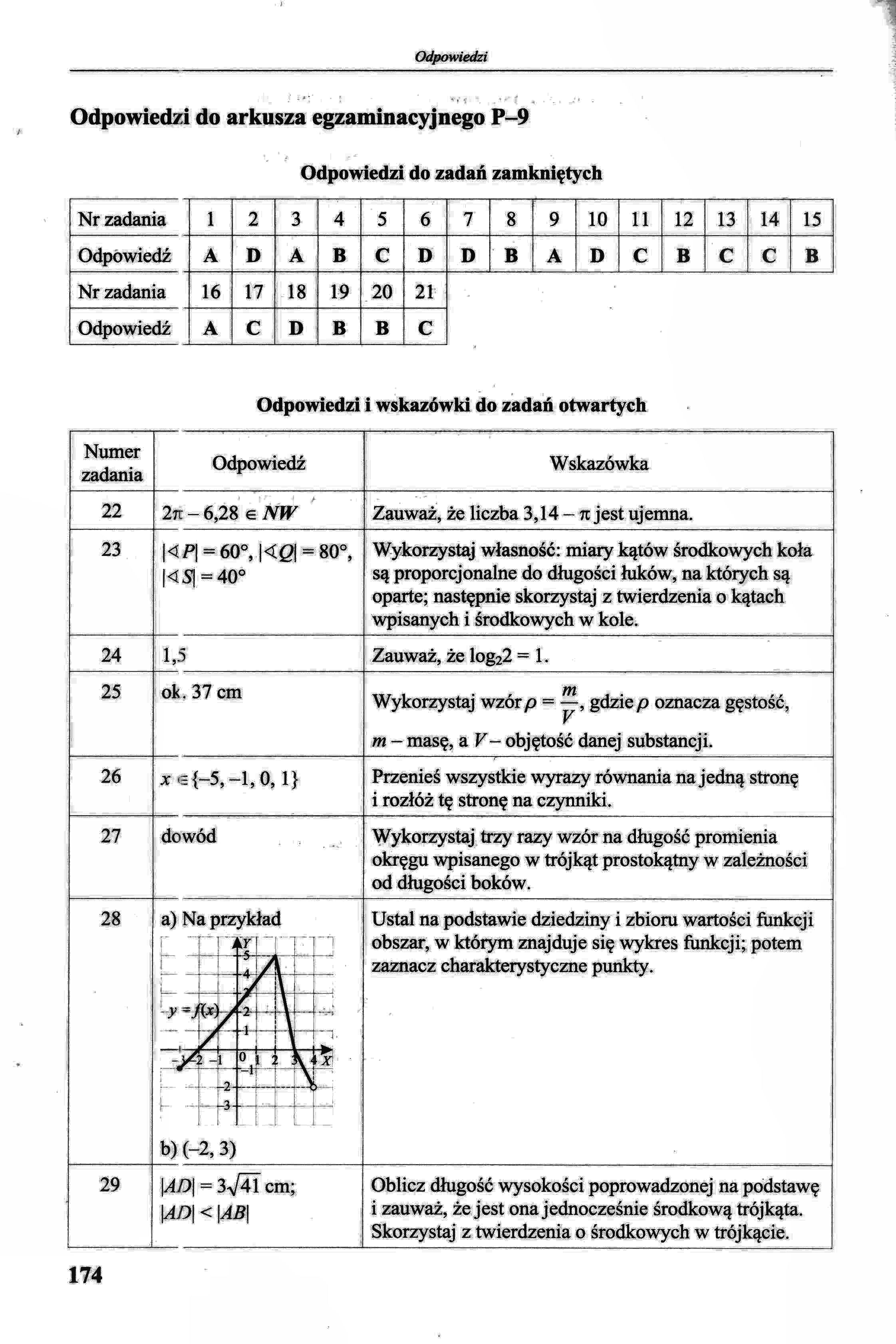
28	a) Na p |p Tl		irz	ykła< %	i		Ustal na podstawie dziedziny i zbioru wartości funkcji obszar, w którym znajduje się wykres funkcji; potem zaznacz charakterystyczne punkty.
			_ /		li 1 "i
				2"' -
				^0j-^:	i kil! ■
	b)(-	i "j*-; 2,3)
29	\AD\ = 3^41 cm; \AD\ < \AB\						Oblicz długość wysokości poprowadzonej na podstawę i zauważ, że jest ona jednocześnie środkową trójkąta. Skorzystaj z twierdzenia o środkowych w trójkącie.

174