19805 Skrypt PKM 1 00134

268

moment maksymalny Af_tw., = 500 [Nm], Dwustopniowa przekładnia zębata “ 1

₄ oraz sprawności ij, «* ą₂ = 0,98. Ma-

J. =    = J₃ = 1 [kgm²],    = 5

500 [N]. Przyjąć

to-

posiada przełożenia /. =

(0_t

bezwładności

wynoszą j, =

[kgm²]. a średnica bębna D = 0,4 [m], ciężar zblocza G założenie, że elementy napędu są nicodkształcalnc.

sowę momenty

,2

Rozwiązanie

Zredukowane momenty bezwładności na wał sprzęgła wyniosą w warunkach rozruchu

/_t =J, = 1 [kgm²].

1

+ -Ai +

«£

2,34 [kgm²],

gdzie — jest stosunkiem prędkości podnoszenia do

prędkości kątowej bębna

t

-f-W [«]•

Obciążenie sprzęgła spowodowane ciężarem wyniesie

Mi = (G + G) ?    « 198,4 [Nm],

⁴

(8.30)

a obciążenie związane z przyspieszeniem mas w ruchu obrotowym

(8.31)

(8.32)

M\- = _Sl₂ =    = 211,3 [Nm].

M +

Moment obliczeniowy na sprzęgle S,

M₀, = M\ + Mi' - 410 [Nm]. Analogicznie można obliczyć moment na sprzęgle S₂

(8.33)

|_{2 = j! +} e±5(®)^! _{= }15} [kgm'].

W₂ = (C + C?)- = 3050 [Nm],

M_2auiM = M_lau ~r^ = 7840 [Nm].

V¹!

Mi = -Ą-(M_2m., - Mi) = 1740 [Nm].

i, + J₂

M₀₂ = Mi + Mi = 3050 + 1740 = 4790 [Nm].

Odpowiedź:

Momenty obliczeniowe na sprzęgłach S, i S₂ wynoszą M₀, =410 [Nm], M02 = 4790 [Nm].

Zadanie 8.9

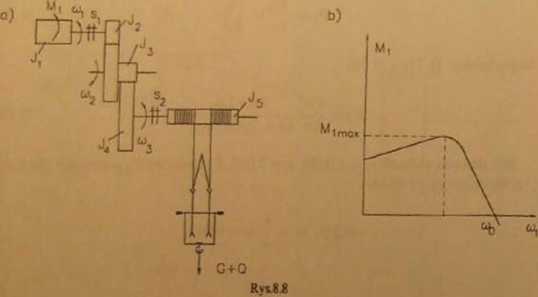
Dla układu, jak na rys. 8.8, zbudować model obliczeniowy pozwalający uwzględnić odkształcalność skrętną sprzęgła S, o sztywności c, oraz lin stalowych o sztywności c₂. Napisać równania opisujące drgania w układzie napędu przy poderwaniu ciężaru Q + G, pozwalające na obliczenie sil dynamicznych w sprzęgle S, i linach stalowych. Wiadomo, że model dynamiczny silnika asynchronicznego można opisać równaniem fl₀co₀ + c₀(p₀ - <p_k) = 0, gdzie /?„, c₀ -stale, <j>₀ = ui₀ — prędkość kątowa wirowania pola magnetycznego. 9, — prędkość kątowa wirnika.