62322 Skrypt PKM 1 00104

208

Rozwiązanie

Maksymalne naprężenia radialne dla tulejki i głowy korbowodu występują na średnicy D (rys. 6.2) i wynoszą

o,i = o_r2 - -Pm = -45 [N/mm⁵], [MPa]

Naprężenia obwodowe

Największe naprężenie obwodowe w tulejce występuje na średnicy otworu d

o,i = p^d + kj = 45(1 + 1,96) = 133,2 [MPa].

W głowic korbowodu największe naprężenie mamy na średnicy D

o,i = Pn»,k₂ = 45-2,72 = 122,4 [MPa].

Sprawdzenie warunku wytrzymałości tulejki i głowy korbowodu

Tulejka. Zgodnie z tabl. 6.3 dla materiałów ciągliwych oraz drążonego czopa

g- - 0,58(1 — Xi),

^K*1

zatem

p_t = 0,58R_gl(l -x{) = 0,58-200(1 - 0,57²) = 783 [MPa].

Ponieważ p, > p_mu, warunek wytrzymałościowy dla tulejki jest spełniony. Głowa korbowodu

£- = 0.58(1-*I).

p₂ = 0,58 *.₂( 1 - x\) * 0,58 • 1200(1 - 0,68²) = 321,8 [MPa].

W tym przypadku również warunek wytrzymałościowy jest spełniony Pi > Pm** — 45 [MPa].

Zadanie 6.3

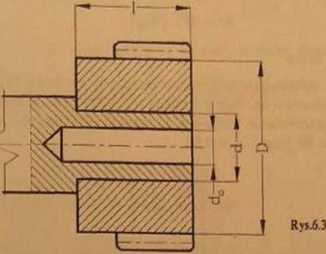
Obliczyć maksymalny moment obrotowy, który może przenieść kolo zębate (rys. 6.3) osadzone z wciskiem W — 0,1 [mm]. Do obliczeń przyjąć: d_t = 10 [mm],

d = 25 [mm], D = 40 [mm], i = 25 [mm], /i = 0,1, £, = E₂ = E = 2,1 • 10⁵ [MPa], v, = v₂. Pominąć wpływ chropowatości powierzchni na wartość ciśnienia.

Rozwiązanie

Współczynniki wydrążenia

*i

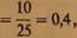
*2

25

40

= 0,625.

Zatem

^ki =

l±ii

1

1 + 0,4² 1 - 0.4²

1,38.

= 2,282.

+    1 +0,625²

’²    1 - 0.625²

Ciśnienie na powierzchniach łączonych ze wzoru (6.7), który dla danych w zadaniu przyjmuje postać

WE

d(*t + kj

0.1-2.1 10⁵

25(1,38 + 2,282)

229 [MPa],

p = 229 [N/mm²], [MPa].