Skrypt PKM 1 00138

276

Rozwiązanie

Równania dynamiki

Ji Pi + c(ę>j - <p₂) + B{(p_i - (pi) = 0,

(8.50)

J₂ p₂ -f c(<p₂ — Pj) + B(g>2 — ę>j) = Mo cos(v t + *©) po podzieleniu odpowiednio przez J, i J₂ i odjęciu stronami dają zależność

Ćj - «>', + C(«>z - <?,)^ + jJ + B(pj -    = ^cos(vt + *o)

Podstawiając

B(± ₊ ±y_S o.    c(± ₊ ±J = „S,

otrzymujemy równanie drgań względnych sprzęgła podatnego w formie

x + ń₀x + o>gx = p₀cos(vt + a₀).    (8.5i)

Amplitudę drgań ustalonych obliczymy, znajdując całkę szczególną (8.51). Łatwo wyliczyć, że

x — A cos»i gdzie tgz₀ = ^.tL    _{(g 52)}

ym *•

Dla

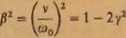
(8.53)

wystąpi amplituda maksymalna (rezonans) o wartości

(8.54)

_A „ P*____¹__

"** o>o    — J²

Odpowie di:

Równanie ruchu względnego zredukowanych mas na wał sprzęgła ma postać (8.51). Amplitudę drgań wymuszonych według (8.52) oraz jej wartość w rezonansie można obliczyć zgodnie z (8.54).

Zadanie 8.12

Napęd głowicy frezarki składa się z silnika asynchronicznego, sprzęgła

podatnego S, przekładni stożkowej o przełożeniu i = oraz wrzeciona głowicy

4

(rys. 8.14). Obliczyć sztywność sprzęgła r, tak aby współczynnik wzmocnienia (wzrost amplitudy drgań skrętnych) był mniejszy od 1. Głowica frezowa wymusza

drgania skrętne o częstości v = —* z, gdzie n₂ - obroty wrzeciona, z - ilość

ostrzy w głowicy. Do obliczeń przyjąć dane: obroty silnika w procesie skrawania n, = 950 [obr/min], J_: = 20 [kgm²]. J₂ « 10 [kgm²], J₃ = 160 [kgnr], z ^ 9.

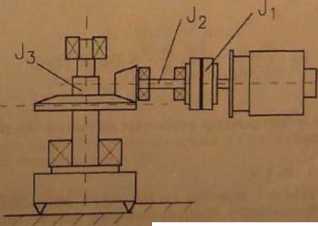
RysJLU