31398 skanuj0026 (111)

4. Zasada prac przygotowanych - wyznaczanie wielkości statycznych. Przykłady rozwiązań

Zasada prac przygotowanych (wirtualnych) odgrywa dużą rolę w statyce układów statycznie wyznaczaJnych (układy izostatyczne). Na podstawie tej metody, nazywanej metodą kinematyczną, można wyprowadzić wszelkie twierdzenia statyki dla tych układów. Metoda służy do badania równowagi; służy zatem do wyznaczania reakcji jak i wielkości sił przekrojowych. Wykorzystuje się tutaj twierdzenie o pracy wirtualnej (przygotowanej L) dotyczącej ciała (tarczy) doskonale sztywnego. Zasada pracy (równanie prac) dla takiego ciała ma postać

L=Z(P.-ŚJ = O-

n

W równaniu tym oznaczono:

P„ — wektor siły uogólnionej

E_n — wektor przemieszczenia uogólnionego (wirtualnego), na którym pracę wykonuje P_n.

Zasadę wysłowimy w następujący sposób: suma prac wirtualnych sił zewnętrznych na wirtualnych przemieszczeniach zgodnych z kinematycznymi właściwościami (ograniczeniami) układu jest równa zeru w przypadku równowagi tych sił. Jest to warunek konieczny i wystarczający równowagi dla ciała sztywnego (swobodnej tarczy sztywnej). Stosowanie twierdzenia o pracy wirtualnej dla pojedynczej tarczy sztywnej prowadzi zawsze do równań identycznych z równaniami statyki. Natomiast stosowanie tego twierdzenia do układu tarcz sztywnych prowadzi do równania, którego nie można otrzymać bezpośrednio z równań równowagi. Można zatem powiedzieć, że jest to metoda wybiórcza (selektywna) wyznaczania interesujących nas wielkości statycznych.

W celu wyznaczenia wielkości statycznej (reakcja, siła przekrojowa) w ustroju izostatycznym należy przeciąć więź odpowiadającą poszukiwanej wielkości i zastąpić ją nieznaną zewnętrzną siłą czynną, która wraz z faktycznym obciążeniem czynnym wejdzie do równania prac przygotowanych. Równocześnie przecięcie więzi przekształca geometrycznie niezmienny układ izostatyczny w mechanizm, któremu można nadać przemieszczenie przygotowane. Mechanizm może wykonywać ruchy, przy czym ruch jednej tarczy determinuje jednoznacznie ruchy pozostałych tarcz. Przemieszczenie wirtualne charakteryzuje się tym, że jest

—    nieskończenie małe;

—    niezależne od sił obciążających tarczę;

—    dowolne ale zgodne z ograniczeniami kinematycznymi, a więc możliwe;

—    niezależne od czasu.

Małe ruchy tarcz interpretujemy jako ruchy wokół środków obrotu, a przesunięcia przyjmujemy stycznie do trajektorii ruchu, to jest prostopadle do promienia obrotu. Dla mochtini/mu sporządzamy plan przesunięć rzeczywistych (PPR), plan przesunięć obróconych (PPO) lub biegunowy plan przesunięć obróconych (BPPO). W przypadku wykorzystania planu obróconego (lub BPPO) można powiedzieć, że praca (wielkość skalarowa) siły na przemieszczeniu rzeczywistym jest liczbowo równa momentowi siły względem końca wektora przemieszczenia obróconego.

Przy obliczeniu pracy przygotowanej, układ sił działających na tarczę można zastąpić dowolnym układem równoważnym, w tym także wypadkową.

W analizie belek prostych i wieloprzęsłowych przegubowych wykorzystujemy plany przesunięć rzeczywistych, wtedy na ogół środki obrotów tarcz względem tarczy podstawowej (fundamentu) leżą na jednej prostej (oś pręta belki). Jako wielkość wirtualną można przyjąć przesunięcie (translacja) lub obrót (rotacja) jednej z tarcz. Do analizy ram i kratownic wykorzystuje się pluń przesunięć obróconych (PPO) lub biegunowy plan przesunięć obróconych (BPPO). Plany przesunięć mogą być także pomocne przy badaniu geometrycznej niezmienności układu.

4.1. Belka wieloprzęslowa przegubowa

Przykład 21. Dla schematu belki wyznaczyć reakcje oraz siły wewnętrzne w charakterystycznych przekrojach. Wykorzystać zasadę prac przygotowanych.

Schemat statyczny y 10kN

2 kN/m		40 kNm
rTTrjT	Mim i
4 m i 2	A . 2 . 5 . 2 .	5F 4 : 4 . 2 .

Mechanizm „V"

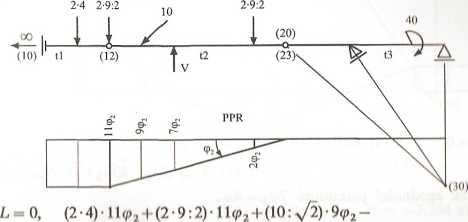
F-7<p₂+(2*9:2)*2ę>₂-0,    +38,377 kN.

71