32889 skanuj0020 (156)

pując go zrównoważonym układem sił osiowych) i wprowadzając do schematu pręt Z. Nowy schemat musi charakteryzować się geometryczną niezmiennością (w ogólnym przypadku łatwą do udowodnienia) i oczywiście statyczną wyznaczalnością. W naszym przypadku otrzymujemy schemat, w którym reakcje pozostają bez zmian. W zmodyfikowanym schemacie wyznaczenie sił nie powinno nastręczać istotnych kłopotów.

Wybrano następujący tok postępowania prowadzący do wyznaczenia sił w prętach kratownicy.

Równowaga węzła    IP_ix = 0, —G_lx+G_2x—Q = 0,    (1)

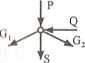
EPty — 0,    — G_ly+G_2y+P+S — 0,

Z geometrii prętów wynika, że

^Glx = _y > ^G2x — 2G_2r

(2)

(3)

Wykorzystując powyższe w równaniu (1) mamy

(4)

— G_iy+G_2y— - Q = 0

Rozwiązując układ równń (2) i (4) otrzymujemy

g_2}=-\p₊\q-\s

oraz G_ly=(5)

Przekrój a-a

2

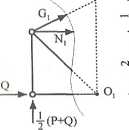
ZM_i0l = 0,

W_l-2+G_1I-3+i(P + e)-2 = 0, N_l-2-3P-jQ-3S+P+Q = 0,

(6)

po wykorzystaniu (3) i (5)

_Nl=P+±Q₊^S.

(7)

Przekrój /?-/?

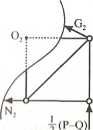
ZM_i02 = 0,

N₂‘2—G₂/2—i(P —0*2 = 0,

(8)

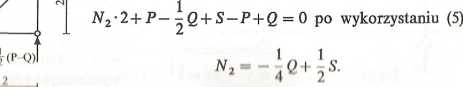
Przekrój <5-<5

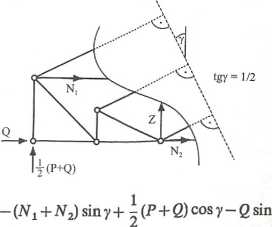
Z =    +Q)tga- ^(J>+0 =

Wykorzystując (9) i (7) w reakcji na Z otrzymujemy

1/1    3    1    1    \1

^{Z =} 2(^P+4^e+2^S-42-2^S-^P) = 2^S’    <">

ale Z = 0 zatem ^iS = 0-»5 = 0.    (12)

Znajomość S pozwala wyznaczyć pozostałe siły w prętach. Dla interesującej nas siły w pręcie D mamy z równania (9).

D = N₂ —

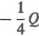
(ściskanie).

Uwaga: otrzymany wynik (S = 0) nie jest zaskoczeniem, bo można go uzyskać drogą superpozycji obciążeń z wykorzystaniem symetrii struktury, 00 pokazano poniżej. Na siatce schematu naniesiono poprawne zwroty nil i opisano wartości sił występujących w prętach.

Stan P

J^p

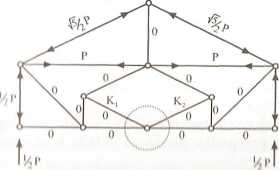
a)    symetria struktury

b)    symetria obciążenia Wniosok: odpowiodź układu symotryczna.

M