34655 Skrypt PKM 1 00063

126

mocowanych na czopie stożkowym W czasie montażu po dokręceniu nakrętki wywołano w czopie siłę rozciągającą równą Q. Obliczyć maksymalne naciski na ściance otworu przy obciążeniu kołka siłą P w czasie pracy sprzęgła. Do obliczeń przyjąć; Q, P. D, d. g. a. p

Rozwiązanie

Na kołek działają równocześnie siły P i Q, które pokazano na rys. 3.25. Poszukując skutku działania siły P redukujemy ją do punktu S środka ciężkości pola przekroju F. Współrzędna środka ciężkości

_gD + ld ^Vt 3 D + d *

Po redukcji otrzymaliśmy silę P wywołującą docisk kołka do ścianki otworu oraz moment

M = P(* + yJ,

który równoważony będne przez naciski.

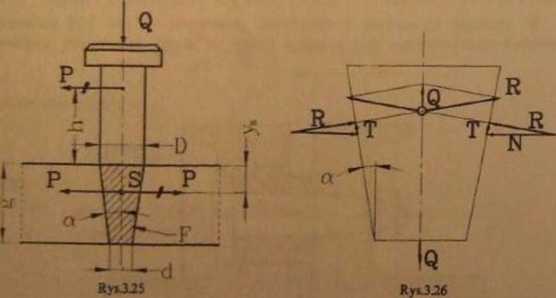
Naciski od siły Q

Rozkład sil na czopie powodowany siłą Q przy uwzględnieniu tarcia pokazano na rys. 3.26. Całkowita reakcja

R

g

2hd(z + py

Reakcja normalna do tworzącej stożka

N-fi co,,--

2 sin (a + p)'

Średni nacisk

2 N iV nF * F *

gdzie

_ D + d f= —₉

Stąd

Pq =

2 Q cos p    ^ Qcosp

7i(Z) + Ą^sin(a + p) ~ (D + d)g sin(a + p)

Naciski od siły P

P cosa 2Pcosa ^Pp ~ F “ (0 + d)fl‘

Naciski od momentu M = P{h + yj.

Do obliczenia nacisków przyjęto schemat obliczeniowy pokazany na rys. 3.27. Moment zrównoważą siły P i P" działające na ramieniu odpowiednio e_x i e₂ względem środka S

P'e_l=re₂

zatem

Af = 2 P e,

Z zależności geometrycznych wynika

sina.

¹    3 cosa \2    /