45131 P1030358

296 M.Polowczyk. E.KIugmann - PRZYRZĄDY PÓŁPRZEWODNIKOWE

6.18. Elementy macierzy [b_e] określa się związkami: ^hlle= ^ubA P«^y U_ce= 0, b_12e= U_bc/U_ce przy I_b= 0,

b₂i_e=IA preyU_cc=0, b₂₂c= Wc prey I_b= 0, gdzie warunek U_ce= 0 oznacza zwarcie zacisków wyjściowych układu, a I_b=0 - rozwarcie zacisków wejściowych tego układu.

Po zwarciu wyjścia układu otrzymujemy schemat równoważny przedstawiony na rys. 6.30, natomiast po rozwarciu wejścia - schemat przedstawiony na rys.15.

Rys. 15

Obliczając na podstawie schematu z rys.6.30 parametry h| ,_c i h_21c otrzymujemy:

^hlle= ^rbb^I+I^gbc⁺j⁽⁰(^CE + C_C)], h₂ie=(gra“ j^(oCC ) /fgbc+M^CE^+Cc)]-Obliczając zaś na podstawie schematu z rys.15 parametry h_12e i h_22c otrzymujemy:

hj2e⁼ J“^Gc / [gbc ⁺    + Cc)],

.    „ gm⁺gbe⁺j°^)CE

^22C"^{SCC J C}8be+MC_C + C_E)'

6.19.

1. Z rysunku 2 wynika:

U

eb

1) h_llb= Rj= 30 Q, bo h_llb - — przy U_cb = 0,

2) h_22b= 1/R₂= 1 pS, bo h<>9_b - 77-przy I_c = 0

U-k

cb

3)    R₃ jest rezystancją wejściową R_we układu WB przy obciążeniu

rezystancyjnym Rq

⁴)    ^R4= *>ue, bo h,_lcprzyU_cc = 0.

2. Analizując układ z rys.2c, przy wykorzystaniu dwugeneratorowego układu

zastępczego macierzy [h_b], co prowadzi do układu zastępczego przedstawionego na rys.16, otrzymujemy:

^h12b ‘ ^2 Ii

^R3"Tr“^hi^,b

U»

„j + ‘    ,

a    m

Rozwiązania zadań 6

Rys. 16

gdzie: U2 — I2 Rq‘» ^2 “ ^21b ^1 ⁺ U₂ ^22b-

Stąd: R₃ - hju, -

R. -

^a12b* ⁿ21b

^h12b ‘ ^h21b

J_ _1_

R₂ Rq

J*o]

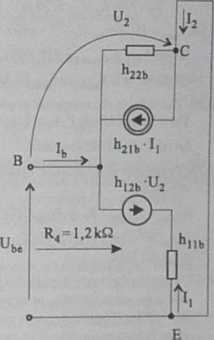
Rys. 17

3. Analizując, z kolei, układ z rys.2d, przy wykorzystaniu dwugcnćratorowego układu zastępczego macierzy [h_b], co prowadzi do układu zastępczego przedstawionego na rys. 17, otrzymujemy:

Ubc	= - u2	= - *>12b	•u2	- ^hiib • ^fi:
Ib=	-Gi +
I2 =	^h21b '^1	[, + b22	•u2.
Stąd
	Ube			^hllb
^hllc	" Ib	"^hlib*	^h22b	+n+h2,b)(i

Uwzględniając w powyższym wyrażeniu to, że:

1)    h_12b « 1 - bowiem wpływ napięcia kolektor -baza na napięcie emiter - baza jest znikomo mały,

2)    hjib• h₂₂b ⁼ 3 ‘ 10"⁵ « (ł + ^h2ib)»

.    •    i    ^hllb

uzyskujemy ^hiie~_1+h2ib

^llb |    < _ n Q7<

skąd ^h2.b-h7~-^,-_R4-¹ -⁰⁹⁷⁵-

4. Parametr hp_b obliczamy korzystając ze znanej

wartości h_2Ib fzależności wyprowadzonej w p.2 zadania, uzyskując przy R₂ = Rq

“I2b = _h

21 b

Rl,R₃

Ro

6,15 • 10 ^S.