57393 skanuj0212 (6)

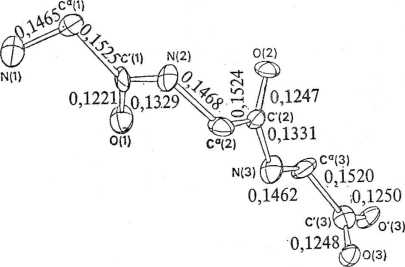
Rys. 2.71. Konformacja organicznego fragmentu addycyjnego związku LiBr • glicyloglicyloglicyna. Fragment ten tworzy^w krysztale jon dwubiegunowy

⁺NH₃—CH₂—CO—NH—CH₂—CO—NH—CH₂—COO"

A. Numeracja atomów j długości wiązań (nm)

B. Kąty walencyjne

N(ł)—0(1)—C'(l)	107,5°	0(2)—C'(2)—0(2)	121,4°
0(1)—C'(l)—N(2)	117,1°	N(3)—C'(2)—0(2)	123,2°
O(l)-C'(l)-O(l)	120,9°	C'(2)—N(3)—0(3)	122,2°
N(2)—C'(l)—0(1)	122,0°	N(3)—0(3)—C'(3)	112,9°
C'(l)—N(2)—0(2)	120,7°	0(3)—C'(3)—0(3)	118,5°
N(2)—0(2)—C'(2)	110,5°	0(3)—C'(3)—0'(3)	116,2°
O (2)—C' (2)—N (3)	115,3°	0'(3)—C'(2)—0(3)	125,3°

C. Kąty konformacyjne (patrz rys. 2.72)

mścienny	pomiędzy płaszczyzną atomów	i płaszczyzną atomów
Wi	N(l)C^a(l)C^/(l)	C*(1)C'(1)0(1)	32°
COi	C^a(l)C'(l)N(2)	C'(l)N(2)C^a(2)	3°
	0(1)C'(1)N(2)	C^,(l)N(2)C^a(2)	— 5°
<P2	C'(l)N(2)C^a(2)	N(2)C^a(2)C'(2) -	-62°
V>2	N(2)C^a(2)C'(2)	C^a(2)C'(2)0(2)	40°
co2	C^a(2)C^,(2)N(3)	C^/(2)N(3)C^a(3)	5°
V2	0(2)C^/(2)N(3)	C^/(2)N(3)C^a(3)	-4°
<P3	C'(2)N(3)C^a(3)	N(3)C^ot(3)C'(3)	-3°
V>3	N(2>)C*0)C'(3)	C^0C(3)C^/(3)O(3)	-1°
V3	N(3)C^a(3)C(3)	C^a(3)C'(3)0'(3)	178°

Stosuje się również inny typ modelu (lub rysunek), gdy chodzi o szczególnie wyraźne przedstawienie rozmieszczenia cząsteczek względem siebie (por. rys. 2.63). Jest to model zwarty, czyli model Stuarta, w którym atomy są odcinkami kulistymi o promieniach równych promieniowi Van der Waalsa. Jeżeli istotnie w krysztale występuje zwarte ułożenie cząsteczek, zbudowane w podany sposób modele powinny umożliwiać bezpośrednie stykanie się cząsteczek, co sprowadza do minimum zajętą przestrzeń.

Gdy kryształ jest zbudowany z cząsteczek chiralnych i zawiera tylko jeden izomer optyczny, nie można określić konwencjonalnymi metodami [bezwzględnej konfiguracji cząsteczki, lecz stosuje się do tego metody bardziej skomplikowane (patrz część 4), opracowane przez J. M. Bijyoeta i jego szkołę.

214