64840 skanuj0294 (3)

oraz

F =

(11.69)

cosa₀ cosa₀-cos/?

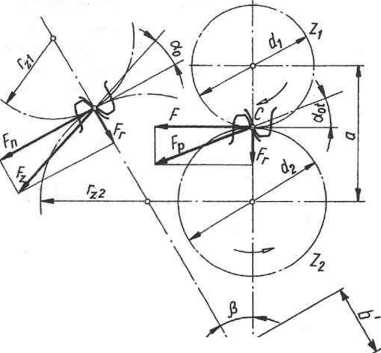
Siły te działają na odcinku b' długości zęba równym

=    (11.701

cos p

Stosunek długości zęba b’ do szerokości uzębienia (wieńca) b jest taki sam, jak stosunek siły między-zębnej F_z do siły zginającej F_n. Zależność tę można określić również w ten sposób, że obciążenie przypadające na jednostkę długości zęba pozostaje niezmienne dla obu rodzajów zębów (prostych i skośnych). Oznacza to, że do obliczeń wytrzymałościowych zębów skośnych można stosować wzory przyjęte dla zębów prostych, pod warunkiem, że wstawiając do wzorów wartość siły F, wstawi się wartość szerokości uzębienia b, a nie długość zęba b'. Wpływ nadwyżek dynamicznych i przeciążeń ustala się również przez wprowadzenie siły obliczeniowej F_obl.

W kołach o zębach skośnych należy sprawdzić wartość liczby przyporu, ponieważ zęby skośne wchodzą w przypór i wychodzą z przyporu stopniowo, a nie całą szerokością, co powoduje zwiększenie liczby przyporu (zależnie od wielkości kąta /?). Wpływ kąta /? na zwiększenie liczby przyporu określa się za pomocą współczynnika, zwanego skokową liczbą przyporu

b-sinB

^P    (11.71)

4 f• y	i i
fv, \4	rr j>
^11 li i v>* ! 1 ■ iiX \
	7 n-

Rys. 11.20. Rozkład sił w przekładni walcowej skośnej

£„ =

m-7i

Całkowita liczba przyporu wynosi wówczas

£_c = £ + £_s    (11.72)

Jeżeli £_c 2, wówczas przy wyznaczaniu siły obliczeniowej F_obl (wzór 11.45) należy przyjąć K_E = 2.

Na podstawie wzoru 11.47 siła obliczeniowa dla kół skośnych wynosi

2M_m 2M_m ■ cos/i

r obi ~ j ~    ~    (11.73)

m- z

Wówczas warunek wytrzymałości na zginanie przyjmie po

stać

294