65447 Nowy 11 (6)

tuiy lusuwe

tuiy lusuwe

(1.44b)

/?_xy(x) = £'[.t(0>’(/-T)] = } \ x,y,_^ p(x_ly_l__x)dx_ldy,._x

-oo -oo

ykładowo, obliczając C_xy(x) należy najpierw wyznaczyć wartości oczekiwane x, i y,__x hwilach czasowych t i t-x dla obu zmiennych x, i y,^ (czyli wartości „średnie” po zbiorach izacji w chwilach czasowych t i t-x), a następnie odjąć je od obserwowanych zmiennych 'wych i obliczyć wartość oczekiwaną (po zbiorze realizacji) ich iloczynu. W tym celu rży znać łączne prawdopodobieństwo p(x,y,-_T) wystąpienia określonej wartości iloczynu

-X'

analizy częstotliwościowej sygnałów losowych stosuje się funkcję gęstości widmowej cy. Jest ona zdefiniowana jako transformacja Fouriera funkcji autokorelacji:

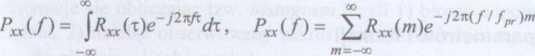
rw iązku z powyższym, prawdziwe są „odwrotne” zależności:

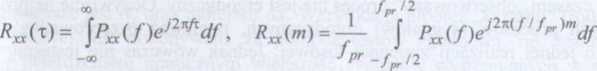
(1.45a)

(1.45b)

i równań (1.45a), (1.45b) nosi nazwę równań Wienera-Chinczyna dla sygnałów ciągłych skrętnych. Ponieważ funkcja autokorelacji jest symetryczna względem t = 0 (R_xx(x) = P_xx(J) jest rzeczywiste, gdyż tylko symetryczne względem zera funkcje cos(2nft) są ■jebne do rozwinięcia harmonicznego /ł„(t). Można wykazać [Hayk98], że dla ciągłych r iłów stacjonarnych, ergodycznych funkcja gęstości widmowej mocy jest równa:

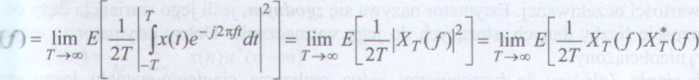
(1.46a)

me £[.] oznacza wartość oczekiwaną, X₇{/) jest transformatą Fouriera fragmentu sygnału -'zedziału czasowego [-T, T] (czyli widmem amplitudy tego fragmentu), funkcja

1 ' X₇(j)\² nazywana jest zaś periodogramem i ma taki sam wymiar jak funkcja widmowej n'.:«ści mocy. Natomiast dla dyskretnych sygnałów stacjonarnych mamy:

2

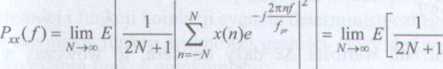
|*,v(/)|²

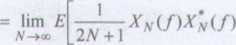
(1.46b)

iwr- przypadku periodogram jest zdefiniowany jako 1/(2A^+1) |A'_a(/)|². Wzór (1.46b) stanowi ajsawę praktycznych metod szacowania wartości funkcji P_XX(J), na przykład metody Welcha, arej w dalszej części tego rozdziału.