79940 P4250038

36

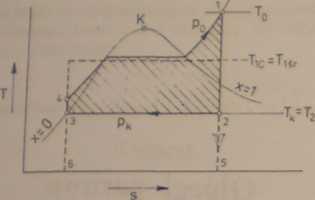
Rys. 112 Obieg idealny Clausiusa-Rankinc'a w układzie T—s

W kondensatorze następuje izobaryczne skraplanie pary i oddanie na zewnątrz ciepła

Kondensat o ciśnieniu p_k podawany jest do kotła pompą zasilającą, sprężającą wodę do ciśnienia kotłowego p₀. Praca jednostkowa pompy

| - k - = U-h-

Praca obiegu CR równa się różnicy między pracą turbiny i pracą pompy

/ - |pg = (/₀-»*)-(/_wr-ii).    (11.1)

Wielkość ta odpowiada powierzchni zakreskowanej na rysunku II.2: 3-4-1-2-3.

Ważnym wskaźnikiem energetycznym jest sprawność obiegu idealnego CR, przedstawiająca stosunek pracy obiegu do ciepła dostarczonego do kotła:

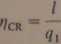
IRi

Wyrażenie (II.2) można napisać w postaci

_n (h-i/J- faz-t*) Oo $) (*w» *i)

Zaniedbując pracę pompy otrzymujemy wzór przybliżony, często stosowany w literaturze do rozważań poglądowych

*?CR rfcR —

JjL

9io

^ł0 ~ *k

*o-*V

(II.3)

Udział pracy pompy y/_T jest rzędu 1-2%, przeto różnice między i tfct $ą niewielkie.

Entalpia pary wodnej nie da się obliczyć w prosty sposób. Można ją odczytać z tablic parowych lub wykresu entropowego jako funkcję ciśnienia i temperatury (lub ciśnienia i stopnia suchości):

f = i(p, t) lub i = i(p, x),

lub znaleźć z kalorycznego równania stanu za pomocą obliczeń numerycznych, wspomaganych ewentualnie komputerem. Do obliczeń wstępnych wystarczającą dokładność otrzymujemy stosując wykres Molliera i—s.

Entalpię kondensatu można oblićzyć ze wzoru

™ ^cw’*k»

gdzie t_k — temperatura kondensatu w *C, zaś ciepło właściwe kondensatu c_w = 4,18 kJ/kg- °C.

Pracę pompy wody zasilającej z dostateczną dokładnością wyraża zależność

4

^lP = lw*-'k - f vdp w v'_k (p₀-P)t).

3

gdzie i/_k = 0,001 m³/kg. W przypadku turbin kondensacyjnych p_k < p₀,

/ ta v'_kp₀. Określając p₀ w MPa otrzymujemy od razu pracę pompy w kJ/kg, równą liczbowo ciśnieniu p₀. Na przykład dla p₀ — 100 bar = 10 MPa, praca pompy wynosi l_p « 10 kJ/kg.

W obszarze wysokich ciśnień należy uwzględnić ściśliwość wody, tj. zmienność objętości właściwej wody v w funkcji ciśnienia p.

2. Wpływ parametrów pary na sprawność obiegu CR

Ze wzoru (II.3) wynika, że sprawność rj_CR jest funkcją entalpii i₀, i_k, i'_k. Skoro

i'o = »'o(Po. *o)» h = h(Pk> Po» ^Jo)» ile = ii(P*)»

przeto

CR * ty CR —f(Po> *0» Pk)*

czyli zależy od mierzalnych parametrów początkowych — ciśnienia p₀ i temperatury t₀ oraz od ciśnienia końcowego p_k.

Analizując wpływ tych trzech wielkości na sprawność obiegu idealnego, celowe jest zastąpić obieg Rankine'a równoważnym sprawnościowo obiegiem Carnota. W przypadku bloków parowych kondensacyjnych odprowadzenie ciepła w kondensatorze odbywa się przy stałej temperaturze, równej temperaturze nasycenia przy ciśniniu p_k, t_k = t„(p_k), co odpowiada warunkom cyklu Carnota. Doprowadzenie ciepła w kotle zachodzi izobarycznie przy temperaturze zmieniającej się od t_wg do t₀ według linii 4 — 1 na rysunku II.2.