s38 39

38

38. y' — arcsin# -f

X

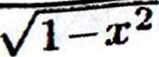
39. y' =

2 arcsin x \/l—x²

40. y' = sina; arctgx + xcosx arctgx +

—2x² (1+a;*)*

3 In² x

X

41. y' =

43. y' =

45. y' — (sin x + x cos x) In x + sin x 47. y' =

42. y' = 0

44. y‘

ln x-fl ln 10

(x² +2x+2)arctg

46. y' = x"(100 lnx + 1) 48. y' = -

x(l + ln x)²

49. y' = 10^a’(l -f #ln 10)

51. y' = e^x(cos# -f sin# -f 2#cosx) 53. y' =

50. y' — e^x(cos# — sin#) 52. y' = 2^X ln 2 cos 2^X

cos# co sx

54. y*

55.    y' = (2x + 3)e^{x2+3x 2}cos(e^{x2+3x 2})

57. y'=(^)^X(ln^-^)

59. y^f = x^smx (cos# ln# +

63. a = 2, 6 = 0

56.    y' = — 3sin(3x)sin(2cos3x)

58. y' = x^x2+1(2 lnx + 1)

60.    y' — (ln x)^x (j^ + lnlnx)

61.    y' = (arctgx)^x [ln(arctgx) + _riT-rf_arct-]

62.    y' — x^x x^x (ln² x + lnx + 1)

64.    k = 0; /'(#) = arcctg^ + dla# ^ 0, /'(0) nie istnieje

65.    Ciągła, oraz /'(0) = 0

66.    Ciągła, /'(0) = 0,/"(0) nie istnieje

67.    Ciągła, /'(O) nie istnieje

68.    /'(O) = 0, /'(O) istnieje, ale /' nie jest ciągła w punkcie # = 0

69.    y = 2#    70. y = 2#

71. y — — \/3(# — f) -f ^    72. y — xe~² + 1

73.    y = — 2x — 1 (styczna), y — \x — \ (normalna)

74.    y = x + 1 (styczna), y = — x -f 1 (normalna)

75.    y = — ~(# — 1) (styczna), y = 3(# — 1) (normalna)

76.    y = 2# — 1 (styczna), y = — |(x — 3) (normalna)

77.    y = rc + 2 i y = x — 2

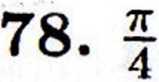
79.

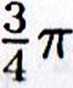
90. v = e-*(8* - t¹ - 15), w = e-*(t¹ - 101 -f 23)

92. E= 1,62

80. Pi(—1,7), P₂(3,-25),

82. Pi (1,0)

84. arctg 3

86. f

88. v = 1, t = oo; v =

81. Pi(0,-2), P₂(-6,4) 83. arctg- i arctg^j

85. arctg 2\/2 87. arctg 3

89. v = 2u, w = 0

91. 33a, 113a

1. Wykazać, że funkcja y = ae^bx spełnia równanie (y')¹ — yy" = 0, gdzie a i b są dowolnymi stałymi.

Rozwiązanie

4P

Obliczając y' i y" mamy:

t/" = ab¹e^bx.

Podstawiając to do lewej strony równania, mamy

= (i/')¹ - yy" = (afce^)¹ - ae^hxab¹e^hx

= a¹b¹e^2bx - a¹b¹e^2hx = 0,

co oznacza, że funkcja i/ = ae^bx spełnia równanie.

2. Dla jakich wartości parametru k, funkcja y spełnia warunek y"(2) = 3.

x¹ — k

x

, a: ^ 0,

Zapisując funkcję ?/ w równoważnej postaci

k

y = x--= x — kx

x

.-i

V

99

2kx ²

1

y' = 1 -f kx ¹,

2

obliczając drugą pochodną, mamy