22470 str007

Tablica 1.2

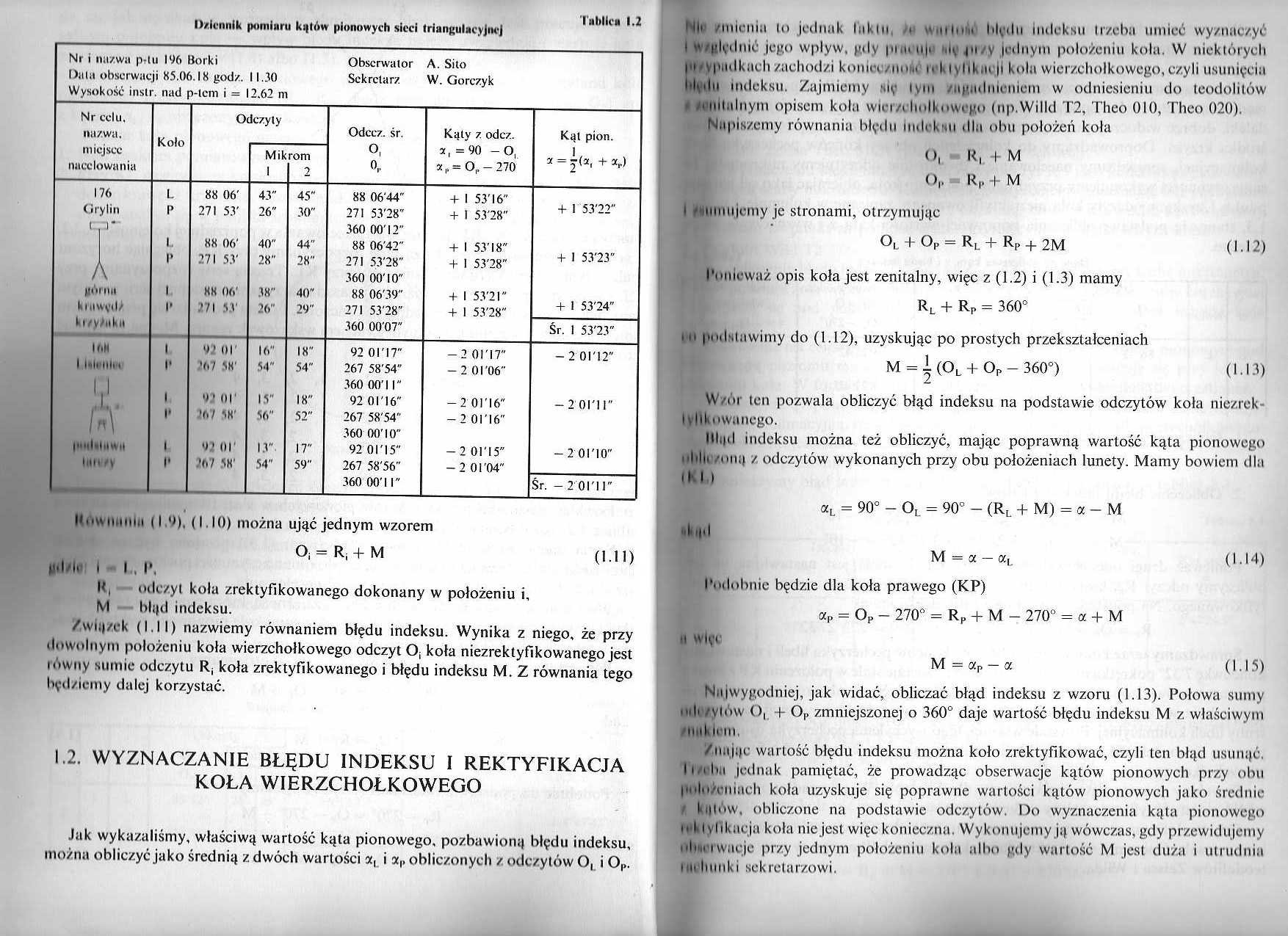
Dziennik pomiaru kipów pionowych sieci triangulacyjnej

Nr i nazwa pitn 1% Borki						Obserwator	A. Sito
Dula obserwacji 85.06.18 godz.				11.30		Sekretarz	W. Gorczyk
Wysokość inslr. nad p-tem i = 12.62 ni
Nr celu, nazwa.		Koto	Odczyty			Odecz. śr.	K<py z odcz. a, =90 -O, st, = 0,-270	Kąt pion.
miejsce mice Iowa nia				Mik 1	rom 2	o, o,		^1 / « = j(a, + a,.)
176		L	88 06'	43"	45"	88 06'44"	+ 1 53'16"	+ I 53'22”
Gry lin		P	271 5.V	26"	30"	271 53'28"	+ 1 53'28"
	l*					360 00' 12"
		L	88 06'	40"	44"	88 06'42"	+ 1 53’18"	+ 1 53'23"
/	\	P	271 5.V	28"	28"	271 53'28" 360 00'10"	+ 1 53'28"
yónm khiwv<)>		1 P	88 06' 271 5,V	38" 26"	40" 29"	88 06'39" 271 53'28”	+ 1 53'2I" + 1 53'28"	+ 1 53'24"
l> • zy>nWi«						360 00'07"		Śr. 1 53'23"
.....		1	92 01'	16"	18"	92 0117"	-2 0117"	- 2 0I'12"
1 l»litllli‘i		1*	767 58'	54"	54"	267 58'54"	- 2 01'06"
1	1					360 00'11"
	l'	1	92 01'	15"	18"	92 0I'I6"	- 2 01'I6"	-2 0l'll"
/	n\	V	267 58’	56"	52"	267 58'54" 360 00'10"	- 2 0116"
piilUllIWlI		1	'» or	13".	17"	92 0115"	— 2 0115"	— 2'0P10"
lnu /y		1'	.'67 58'	54"	59"	267 58'56"	- 2 0104"
						360 00'1 1”		Śr. -2 0I'I1"

l<"" n 111 •. i (I.*)). (1.10) można ująć jednym wzorem

0;=R, + M    (1.11)

jjił/li¹ i I., I'.

K,    odczyt kola /rektyfikowanego dokonany w położeniu i,

M    błąd indeksu.

/ wią/ek (1. 11) nazwiemy równaniem błędu indeksu. Wynika z niego, że przy dowolnym położeniu koła wierzchołkowego odczyt O, koła niezreklyfikowanego jest lówny sumie odczytu R, koła zrektyfikowanego i błędu indeksu M. Z równania tego będ/iemy dalej korzystać.

12. WYZNACZANIE BŁĘDU INDEKSU I REKTYFIKACJA KOŁA WIERZCHOŁKOWEGO

Jak wykazaliśmy, właściwą wartość kąta pionowego, pozbawioną błędu indeksu, można obliczyć jako średnią /.dwóch wartości a, i ot,. obliczonych z odczytów O, i O,..

i III /mieniu to jednak liikm,......1• > I>1.,<Iu indeksu Ir/eba umieć wyznaczyć

< •• /itlędniii jego wpływ, gds pim u|i ,i«. pi/v icdnym położeniu kola, W niektórych (•iMpadkucli zachodzi konia /iu> • • l i, 11k ,u |i kola wierzchołkowego, czyli usunięciu ld\thi indeksu. Zajmiemy mc ivui iigadnicniem w odniesieniu do teodolitów ‘ iiilalnym opisem koła wici a hnlknwrgo (np.Willd T2, Theo 010, Theo 020). Napiszemy równania błędu m>l> kmii dla obu położeń koła

O, R, + M

<),. Rp+M

i aiinnjemy je stronami, otrzymując

o, +Op= R_l+ R_p + 2M    (1.12)

1’onieważ opis koła jest zenitalny, więc z (1.2) i (1.3) mamy

R_l + R_P = 360°

i o podstawimy do (1.12), uzyskując po prostych przekształceniach

M = 1 (O_l + 0_P - 360°)    (1.13)

W,mu ten pozwala obliczyć błąd indeksu na podstawie odczytów koła niezrek i\ Okuwanego.

Itli|d indeksu można też obliczyć, mając poprawną wartość kąta pionowego dilli /oną / odczytów wykonanych przy obu położeniach lunety. Mamy bowiem dla (II)

a_L = 90° - 0_L = 90° - (R_L + M) = a - M

m|i |d

M = a — a,    (1.14)

Podobnie będzie dla koła prawego (KP)

dp = Op - 270° = R_P + M - 270° = a + M

II Więc

M = a_P — a    (1.15)

Najwygodniej, jak widać, obliczać błąd indeksu z wzoru (1.13). Polowa sumy mli stów O, f Op zmniejszonej o 360° daje wartość błędu indeksu M /. właściwym miii k leni.

/nająć wartość błędu indeksu można koło zrektyfikować, czyli ten błąd usunąć, li i bu jednak pamiętać, że prowadząc obserwacje kątów pionowych przy obu p"lii/cniach koła uzyskuje się poprawne wartości kątów pionowych jako średnic kipów, obliczone na podstawie odczytów. Do wyznaczenia kąta pionowego u l lylikacja koła nie jest więc konieczna. Wykonujemy ją wówczas, gdy przewidujemy iiUrrwncje przy jednym położeniu kola albo gdy wartość M jest duża i utrudnia i ni huiiki sekretarzowi.