71701 z3 (20)

f/l_A = 2qa‘a - V_B’a - V_c'2a - qa² -V_D‘3a = 2qa² -6qa² + + 8qa²-qa²-3qa² = O

(spełnione tożsamościowo) potwierdzają poprawność rozwiązania.

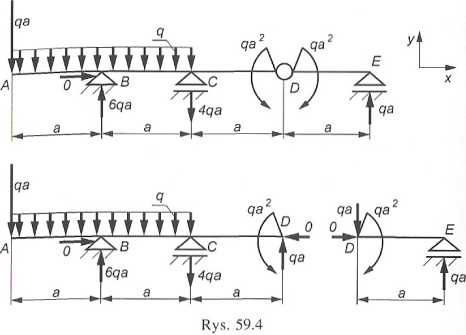
Obliczone wartości reakcji więzów zewnętrznych i wewnętrznych z uwzglęil* nieniem ich rzeczywistych zwrotów pokazano na rys. 59.4. Oczywiste jest, ■ spełnione są (bo być muszą) równania równowagi globalnej, np.

y = -qa + 6qa - 2qa - 4qa +qa =0,

M_d m -qa3a - 2qa *2a + 6qa -2a -4qa-a -qa² + qa² -qa-a 0, ZADANIE 60

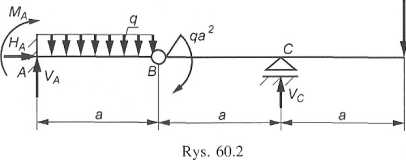
Wyznaczyć reakcje więzów w belce o konstrukcji, obciążeniu i geometrii przedstawionych na rys. 60.1.

iłtłłfłł a*»^z ......Mi
'___L y \ _: ..■■■■ .
/ B a	| Ą a »	^ ^a ►
	Ryg, 6Q,1

|lM#\vii|zanie

Kn/ważana belka (dwuprzęsłowa) zbudowana jest z dwóch sztywnych prętów Ali i BCD. Więzy zewnętrzne to całkowite utwierdzenie w punkcie A j piElparcie przegubowo przesuwne w punkcie C. Nałożonym więzom zewnętrzem towarzyszą reakcje o niezależnych składowych pokazane na rys. 60.2. jlpiPiu rozważana konstrukcja jest zewnętrznie statycznie niewyznaczalna. Jej ■Hirnlny podział na elementy składowe, tj. pręty AB i BCD (cięcie przez ■Rlgub B, tzn. zastosowanie zasady uwalniania od więzów — tu wewnętrznych) Btyłirza sytuację przedstawioną na rys. 60.3. Zatem globalnie do wyznaczenia im nzcść składowych reakcji: V_A, H_A, M_A, V_g, H_B, V_c, do ułożenia zaś — ■Hć równań równowagi (po trzy dla każdej części). Chcąc uniknąć układania Htynitń z niewiadomymi, należy rozpocząć od belki BCD (trzy niewiadome).

(^Hv	TTTłTTf	^8 ! A hb _'		o- (Q O
\ m	a	r Li	^J % a BI a

^yL

X

Rys. 60.3

■ Z równań równowagi:

M_B = qa² + qa •la - V_c'a ■ 0,

^2 M_c = -V_B-a + qa² +qa -a = 0, X = H_B = 0,

but

V_c = 3qa, V_B = 2qa, H_B = 0.

iprowdzenie:

^2 Y ■ -V_B V_c - qa ■ -2qa + 3qa - qa = 0 (spełnione).

151