224 2

224

6. Równania nieliniowe

Ćwiczenie. Obliczyć e„₊i dla n=l,2, 3 w przykładzie 6.4.1.

Załóżmy teruz, że metoda siecznych jest zbieżna. Gdy n jest duże, to    i

(6.4.4)    |Ą,_{+ l}|»C[ą,|'|^-,|

(z tym samym C, które wysiępowało W (6.3.4)). Spróbujemy teraz określić wykładnik zb eż

ności metody siecznych. Przypuśćmy, że

|e*₊1|«K|c_n|^,\    |£_-|«iC|e_n._I|^p.

Podstawiając to do (6.4.4). otrzymujemy równość

Ten związek może być prawdziwy tylko wtedy, gdy p= 1 — 1 //», tzn. gdy p = Hl±_v'S) i C—K^l+i'^p=K^p. Można wykazać, że pierwiastek o mniejszej wartości bezwzglęónej należy tu odrzucić i że

l*,.+i|»C^ł'^,W’ £^dzic    P = ł(l+y5)=l-618...    («3>l).

Powyższe heurystyczne rozważania można przekształcić w ścisły dowód; zob. Ostrowski [83], rozdział 12.

6.4.3. Reguła fałd

Reguła falsi jest wariantem metody siecznych, w- którym — inaczej niż w tamtej metodzie - prowadzi się sieczną przez punkty (x_a,fj i (.*„•,/«'). gdzie n jest największym wskaźnikiem mniej* zym od n i takim, że/„/«*<0. Początkowe przybliżenia x_c i x_x trzeba oczywiście wybrać tak, żeby było fj\ <0. Zaleta metody reguła falsi polega na tym,

•*vV

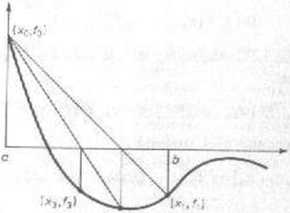
Rys. 6.4.1

że w tym przypadku wszystkie kolejne sieczne będą przechodzić przez punkt l

że — jak metoda bisckcji — jest ona zawsze zbieżna dla funkcji ciągłych/(*)-v/ przeciwieństwie do metody siecznych, reguła falsi ma na ogół wykładnik zbjeżoc ^^ Że tak jest wtedy, gdy f{x) jest wypukła w [x₀. X!], można dostrzec na rys. 6.4.1.    •

0