257 (37)

414

teoretycznie w zależności od kształtu palisady i warunków termodynamicznych.

Elementarny strumień dużych kropli za kierownicą wynosi więc

1X34)

óm_kt m /Jm (l v,,)•/..

W podobnych turbinach i jednakowych stanach ruchu jest X % const. /.układając, że wszystkie krople mają tę samą reprezentatywną wielkość r, powstaje w rozpatrywanym wycinku kanału

kropli na sekundę. Szerokość powierzchni łopatki wirnikowej trafionej tymi kroplami zależy od kształtu palisady i kierunku ruchu kropel w układzie względnym (rys. X. 17).

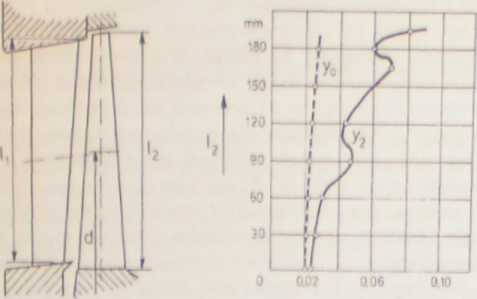
Rys. X. 17. Rozkład zawilgocenia w stopniu wzdłuż promienia według [44]

/

Elementarna powierzchnia bombardowana dużymi kroplami wynosi dla pierścieniowego wycinka wieńca

(X.36)

AS = b_e-AR₂-z₂.

gdzie: AR₂ — wysokość elementarnej powierzchni pierścieniowej, z₂ — liczba łopatek wirnikowych.

Dla jednorazowego równomiernego pokrycia powierzchni AS kroplami o promieniu f potrzeba

(X.37)

kropli. Wobec lego liczba uderzeń w jedno miejsce powierzchni AS, ij. częstość uderzeń na sekundę, wynika z relacji

Wstawiając (X.32) i (X.38) do (X.29) otrzymujemy wzór na wskaźnik erozji

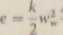
dm (l - x₀W Fas

Wielkość ta stanowi piiarę zagrożenia erozyjnego łopatki zgodnie z przyjętym modelem.

Wskaźnik erozji jest proporcjonalny do gęstości strumienia dużych kropli

na wlocie do łopatek wirnikowych. Na erozję ma wpływ zawilgocenie przed stopniem y₀ = 1— x₀ (a nie zawilgocenie końcowe y₂!). Ponadto zagrożenie erozyjne zależy od prędkości kolizji w¹, i od wyrażenia f-AS.

W literaturze¹ przytacza się zależność wskaźnika erozji od wyższej potęgi prędkości iv_w, co wydaje się prawdopodobne. Jako pewne ocenia się obecnie twierdzenie, że na erozję kroplową ma wpływ jedynie składowa prędkości kolizji normalna do uderzanej powierzchni. W rozważaniach naszych nie zajęto się tym bliżej, gdyż zawsze istnieje element powierzchni łopatki atakowany kroplami prostopadle. Ten właśnie element (część profilu) jest najbardziej narażony na erozję kroplową. Z budowy wzoru (X.39) można by sądzić, że wskaźnik erozji zależy od odwrotności średniego reprezentatywnego promienia kropli r, że ze wzrostem rozdrobnienia fazy ciekłej erozja rośnie.

Mniejsze krople mają jednak większą prędkość bezwzględną c_tt, dzięki czemu kąt fi_lw rośnie i rośnie szerokość powierzchni profilu b_r bombardowanej kroplami, czyli rośnie wyraz AS we wzorze (X.39).

W przypadku bardzo małych ki opel możliwy jest przepływ części strumienia kropli przez kanał międzyłopatkowy bez kontaktu z powierzchnią łopatki (por. rys. X.7b). Ponadto — nie widać tego we wzorze (X.39) — ze wzrostem promienia kropli rośnie pole powierzchni obciążonej uderzeniem jednej kropli. Dla większości materiałów o budowie krystalicznej powoduje to wzrost miejscowego zagrożenia wytrzymałościowego, przy tym samym średnim ciśnieniu kolizji Ap.

Powstaje pytanie, czy liczba uderzeń v (odwrotnie proporcjonalna do promienia kropli r) ma większy wpływ na erozję niż wpływ średnicy kropli. Z badań eksperymentalnych wynika, żc „współczynnik materiałowy” k we wzorze na wskaźnik erozji (X.29) i (X.39) zależy nie tylko od rodzaju materiału,

1

K rz) żanowski J„ Szprcngio! The I' lluence of Droplel Size on the Tiirhine Bladlng Erosioi; Hazard, Trans. ASMF., J. of Hng foi Power. Oclobcr 1978, 100. s. 561 — 565.