294 (28)

- 294 -

drugim etapie obliczamy wielkości sterujące, a mianowicie

^U1 ⁼ +JtoŁ ^E‘

tawiając (2) do d) ostatecznie otrzymamy

o.²R₂LCk_uu

^U2    + j Coli) u + jcoK,C; ^E*

<2)

0)

- 295 -

_uj_ąC układ równań (2) dostaniemy

~^kIU^R1^R2 * J^a;C2^R1^R2_ j

2    — co R-jR^C-jC^ + j£uR.j (C₁ + C₂ + kjyR₂C₂)

pod®*®*

. _c rt_ane i wykonując obliczenia otrzymamy

V₂ » 6,4 \[2

j5°12'

a po podstawieniu danych

, ,obec tego

3.92    J123°42'

^U2 “ ^e'

v₂(t) = 12,8 aindOOOt + 5°120 V.

Stąd

u₂(t) = 3,92 aindOOOt + 123°18^ V.

Zadanie 3.53

Stosując metodę potencjałów węzłowych do obwodu przedstawionego oa ». 3.53.1 uzyskamy następujący układ równań

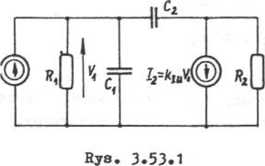
l    -iooC_zV, + (£- + jcuC₂)V₂ - -x₂

^lR7 ⁺ icuC1 ⁺ J«"C₂)v₁ - ja.c₂v₂ = i_a

^I2 ^{= k}IU⁷1*

w./łwnie 3.54

Równania prądów Oczkowych dla obwodu z rys. 3.54 są następujące

^H +	i_ j^C	0
1	o 2	1
	^R + JZTC	^-
0	- J—» R JuiC	^+

-*uu^V

0

0

11)

(1)

Podstawiając tę zależność do 0). otrzymamy i

⁽H7 ⁺ 3^WC1 ⁺ 3^^C2^^V1 - i^^c2⁷2 ^{3 I}s«

^(-kIU ⁺ ^^C2^)V1 ⁺ (iq ⁺ J"°2> - °-

to zauważyć, że macierz admitancyjna układu (2) nie jest mad^erZ^ ryczną.

12)

»r

•yrasając V przez dostaniemy

(2)

•'odstawiając (2) do (1) i dokonując przekształceń otrzymamy układ równań

jednorodnych

R . 1 1 ^R + jz* ~ 7Z?	^kuu	^xi		0
jo.C ^R + j ujC	1 juTC	^12	=	0
0 - J-— L	^R + jbn	?3.		0

(3)

jerowe rozwiązanie istnieje, jeśli wyznacznik główny jest równy zero.

■ob_6c .

*®go otrzymamy