MATEMATYKA152

294 V. Całka oznaczona

5. Obliczyć pole figury określonej nierównościami;

a) x²-x£y£3x-x²,

c) y²£x+3, y²S5-x, c) y²£16x\ x£2,

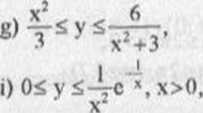
b) x²-xśy<_t‘j2x,

d) x² +y² +6x£0, y²+3x£0, 0 0£ y Sxc~\

^h)

x +4

6. Obliczyć objętość bryły powstałej w wyniku obrotu dokoła osi 0x figury ograniczonej liniami

a) y=Vx,x=4,y=0.

c) y=lnx, x=e, y=0,

g) y = ^3x-x\ y=0,

b) y-cosx dla x€<-x/2,7t/2>, y=0, d) y=arcsinx, x=l, y=0.

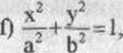
l)    y=3-x², y=2,

m)    y = >/xc'\ y=0.

n) y=^    x>0, x=0, y=0,

h) x²+y² = r², j) y²=2px, x=p>0,

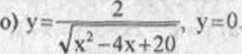
7. Obliczyć objętość bryły powstałej w wy niku obrotu dokoła osi Oy figury ograniczonej liniami:

a) x=y²,x=0,y -2,y=2, b) y=c~'^!* dla x£0,x ^0,y^ 0,

K. Obliczyć pole powierzchni powstałej w wyniku obrotu dokoła osi 0x linii o równaniu:

a) y = Vx,0<x£2, b) y² = 2px,Osx£p, c) y = cosx_?0sx£x/2,

d) y = ya(e^s,;*+e ^x/"),-aśx£a» e) x^2/, + y^2/1 = r^2/\ -rśx£r,

Oy=c ^x|, g) y = 2x\ 0£x£l, h) y = V2x-x².

9 Obliczyć pole powierzchni powstałej w wyniku obrotu dokoła osi Oy linii o równaniu:

a) x = y^,dla -Iśyśl, b) x²+(y-r)² = r² dla 0£y₀£y:Sr.

Odpowiedzi.

1.    a) -~J2+jln( 3+2^2), b) w»k.: aprowadzić do ćwiczeń ia a) przyjmując y jako zmienną niezależną, <0 14/3, d) 37, c) (31^31-8)/27, I) (c‘ +l)/4.

_g) l_a(e-e-'). h)3+jln2, i) 3ln5-2, j) 31n5-2, k) jln3, 1) 2x,

I) 2(V2 -1), 2, 4; m) 2, n) lf2.

2.    a)lj2/$. b) 10, c)2x^:r, d)8r, wskazówka: lx'(0]²+fy'(01²« 2r(l+cost)*

P _

=4r²cos²(t/2>, c)6r, 0 2*Vr²+k² , wsk.: W= J^|x'(t)|²+[>"(0]²-Kz'(l)]²dt,

a

■ g) 4/3, h) e-e"¹.    _ _

3.    o)2*r. b) 2nr, c)3w/4, d)4r, e) yatfWd*²+1 +ln(2x+V4x²+Dh

4 a) 20—, b) 8, c) 8, d) 8/3, c)1,5-2ln2, 0 6ln3. g)7/6, h) 4p²/3, i) rcab, j) 1, k) % , 1) x , 1) I. m)l.

5.    a) 8/3, h)2, c)64/3, d) l2-t-9sc/2. 0W2/5. 01. g) (3x-2)/>/3 , h) k ,

6.    «)8jt.^J>b) *²/2. c)t(«-2), d)K(it²-8)/4, e)*²/2. 0 4iwb²/3. g)9x/2,

h) 4wV3. i) ic(it²-4), j) iq>\ k)xe^J. I) 32*/5. l)2x². m)x/4. n)*/2. o) x².

7.    a) 64it/5, b)32x.

8 a) 13x/3, b)2xp²(3>/3-l)/3. c) *^2+ln(l+V2)l, d) xa^:(2+sinh2). c)I2iu²/5. 0«^+l'KI+^)). g) 37^37 jc/m, h) 4ic. a) 2n(10yi0-l)/27. b)2xr(r-y₀).

9.