MATEMATYKA150

290 V. Całka oznaczona

TWIERDZENIE 4.6 Pole |S( powierzchni S (rys 4.13), powstałej w wyniku obrotu dokoła osi 0x krzywej y = f(x), a £ x <, b, gdzie f jest funkcją klasy C¹ na przedziale < a, b >, wyraża się wzorem

(4 7)    |S|=2nJ|f(x)|Vl+[f’(x))^łdx.

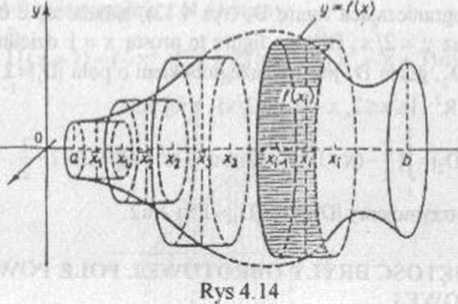
Nie podaliśmy tu definicji objętości |Vj i pola JS| i nic dowodziliśmy twierdzeń 4.5 i 4.6, ponieważ byłoby to postępowanie zupełnie analogiczne jak przy wyznaczaniu pola trapezu krzywoliniowego, pracy w fizyce (por. paragraf 1), czy długości luku w tym paragrafie. Definiując objętość |V| należałoby przybliżać bryłę V, (rys 4.14), walcami

o wysokościach h, = Ax_; i promieniach podstaw r,-Jf(x₍)|, sumować objętości tych walców i przejść z ich liczbą do oo; łatwe obliczenie tej granicy prowadzi do wzoru (4,6).

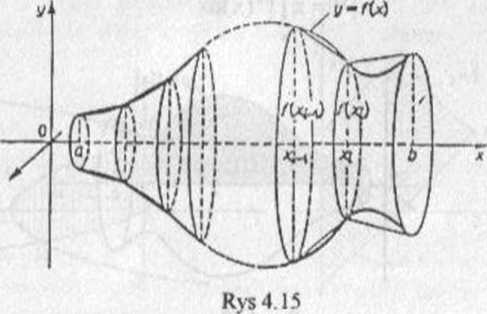
Podobnie przy definicji pola |S| należałoby powierzchnię obrotową przybliżać stożkami ściętymi jak na rysunku 4 15; tym razem obliczenie granicy sum pól powierzchni bocznych tych stożków byłoby o wiele trudniejsze.

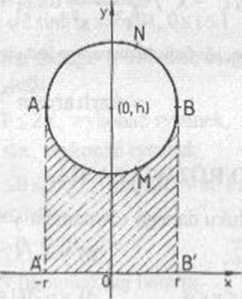
PRZYKŁAD 4.7 Toruscm nazywa się bryłę powstałą w wyniku obrotu kola (rys 4.16) dokoła osi leżącej w płaszczyźnie koła i mc przecinającej go. Toruscm jest np dętka pojazdu kołowego. Obliczy my a) objętość i b) pole powierzchni torusa wykorzystując wzory (4 6) i (4 7).

Rys 4 16

a) Niech obracające się koło będzie opisane nierównością x^r+(y h)²śr^J, 0<r<h, (por rys4 16)

Niech V, i V₂ oznaczają bryły zakreślone przy obrocie odpowiednio trapezów'. A’B'BMA i A'B'BNA Łuki AMB i ANB mają równania

y = h-VP-x², -r£x£r _oraz y = h + Vr-x², -r£x <,r. Przy tych oznaczeniach znajdujemy objętość |V| torusa V:

|Y|=jV₂f-|V,|={wzor (4.6)} = 7t||h+>/r -x^: | dx—7t j|h—Vr*"~x² J^:dx =