MATEMATYKA127

244 V. Całka oznaczona

TWIERDZENIE l.l (warunek konieczny calkowalności). Jeżeli f jest funkcją całkowalną na przedziale <a,b>, to f jest ftinkcją ograniczoną na tym przedziale.

Twierdzenie to orzeka, że ograniczoność firnkcji jest warunkiem koniecznym jej całkowa!naści.

TWIERDZENIE 1.2 (trzy warunki wystarczające całkowalnośa) Jeśli spełniony jest dowolny z następujących warunków;

(1)    funkcja f jest ciągła na przedziale < a, b >,

(2)    funkcja f jest ograniczona na przedziale <a,b > i ma w nim skończoną liczbę punktów nieciągłości,

(3)    f jest funkcją monotoniczną na przedziale < a, b >, to f jest funkcją całkowalną na przedziale < a, b >.

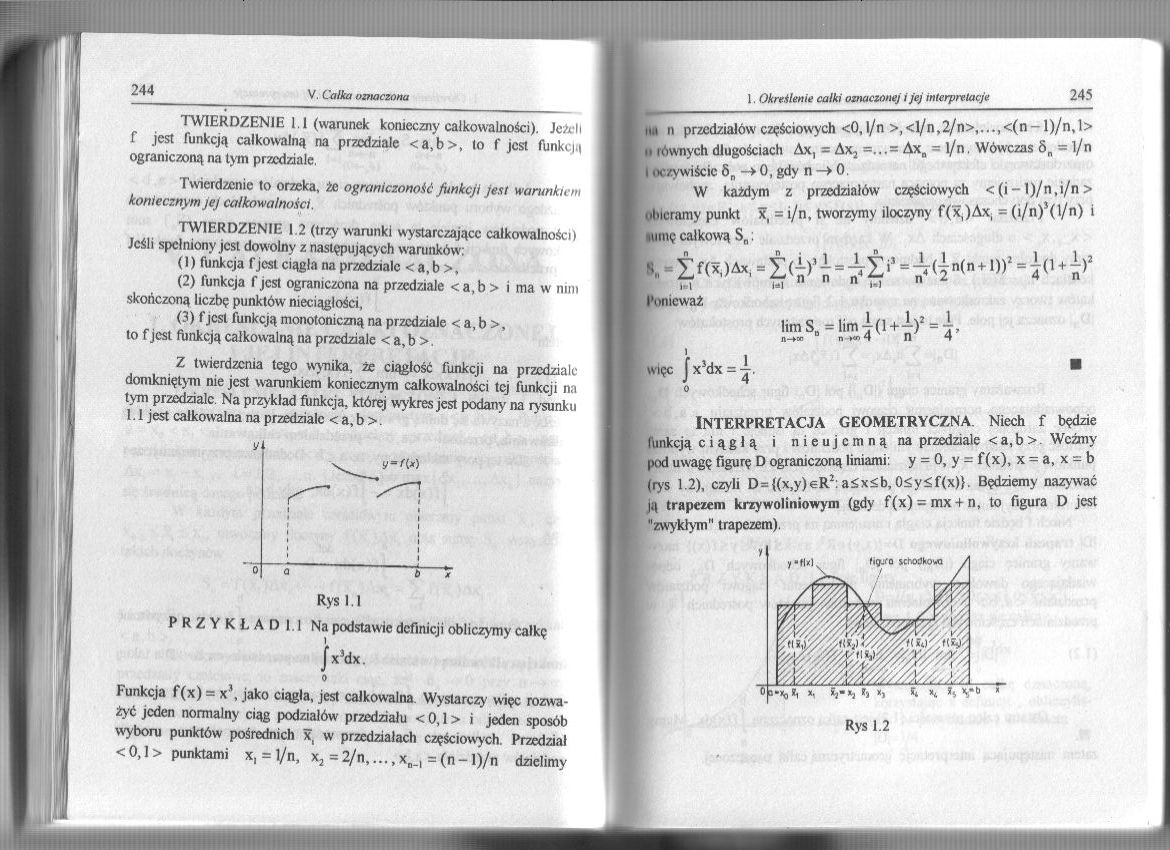
Z twierdzenia tego wynika, że ciągłość funkcji na przedziale domkniętym nie jest warunkiem koniecznym całkowalności tej funkcji na tym przedziale Na przy kład funkcja, której wykres jest podany na rysunku 1.1 jest całkowalna na przedziale < a, b >.

0 Q

6 »

Rys l.l

PRZYKŁADU Na podstawie definicji obliczymy całkę

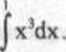
o

Funkcja f(x) * x\ jako ciągła, jest całkowalna Wystarczy' więc rozważyć jeden normalny ciąg podziałów przedziału < 0,1 > i jeden sposób wyboru punktów pośrednich x, w przedziałach częściowych. Przedział <0,1> punktami x, = 1/n, x₂ = 2/n,..., x₀_, = (n- l)/n dzielimy

im n przedziałów częściowych <0,l/n >,<l/n,2/n>,...,<(n - l)/n,l>

. równych długościach Ax, = Ax₂ =...= Ax₀ = l/n. Wówczas 6_n = l/n \ oczywiście 8_n -» 0, gdy n —> 0.

W każdym z przedziałów częściowych < (i - l)/n,i/n > obieramy punkt x₍ = i/n, tworzymy iloczyny f(x₁)Ax, = (i/n)'(l/n) i •urnę całkową S₀;

M    i-l ¹    n ł-1 n

Ponieważ

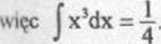
o

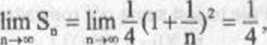
Interpretacja geometryczna Niech f będzie

funkcją ciągłą i nieujemną na przedziale <a,b>. Weźmy |kx1 uwagę figurę D ograniczoną liniami:    y = 0, y = f(x), x = a, x = b

(r>’s 1.2), czyli D = {(x,y)€R²: a^x<b, Ośy<f(x)}. Będziemy nazywać ją trapezem krzywoliniowym (gdy f(x) = mx + n, to figura D jest "zwykłym” trapezem).

Ua-K,,*, x, >>«, r, «,    ^ \ h V^b *

Rys 1.2