MATEMATYKA144

278 V Całka oznaczona

«o    fl

J4rdx = lim J4rdx = lim ^(P¹'” - D = +<*>■

J x p »*w*j x p »t<» i —a

CC

Dla a > 1 całka J -~dx jest zbieżna, ponieważ

I

no

f~-dx = lim tJ-(P' ^a-!)*■—

J x° M*l.ra    l~ot

1

Z kryterium całkowego wynika zatem, że szereg - jest zbieżny, gdy

n»l *

a > l albo rozbieżny, gdy 0 < a < l.

b)    Mamy tu a₀ = l/(nlnn), więc f(x) = l/(xInx). Na przedziale < 2, oc) funkcja f jest malejąca i dodatnia. Ponieważ

li^{dx =} &l4^{dx =} tJ ^ln(lnP)^_|n(ln2))=+=°.

2 2

<*> H    1

więc całka j jest rozbieżna. W konsekwencji szereg ńlrtct ^^CSl

2

rozbieżny.

c)    Mamy tu f(x) = -f—więc a₀ = f(n) =    .

Funkcja f jest malejąca i dodatnia na przedziale <l,oe). Badamy zbieżność szeregu

f-ęJL

Łatwo sprawdzić (korzystając np z kryterium porównawczego lub z kryterium Cauchyc'gO), że jest to szereg zbieżny Z kryterium całkowego wynika, że rozważana w zadaniu całka niewłaściwa jest zbieżna. ■

ZADANIA DO ROZWIĄZANIA

1. Obliczyć całki niewłaściwe (lub ustalić ich rozbieżność), w punktach b), c), d) podać interpretację geometryczną

g)f r*' ",    h) fln^:xdx,    i) a > O, a > 0.

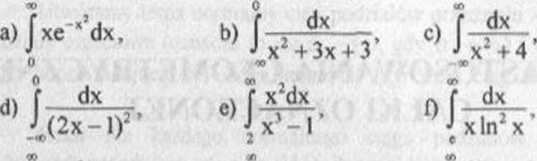
2 Obliczyć całki niewłaściwe (lub ustalić ich rozbieżność), w punktach a), b), c) podać interpretację geometryczną:

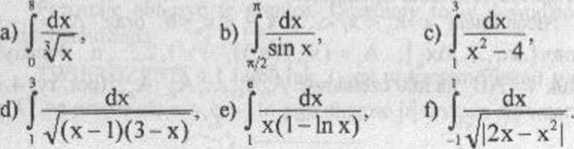
3. Zbadać zbieżność całek niewłaściwych:

4 Zbadać zbieżność szeregów:

Odpowiedzi,

I u) 1/2, b) 5n/(W3). c) n/2, d) 1/2, e)rcabicżna, 0 I. g) (ln7)/3, h) rozbieżna, i)t»^,"^<*/(a-l)dla o>I, rozbieżnudlu otsl 2. u) 6, b) rozbieżna, c) rozbieżno, d) n , e) rozbieżna, 0 */2-ln(2-V3).

3    a), b),c), f), g), i)-zbieżne, d). c), h)- rozbieżne.

4    a) rozbieżny, b) zbieżny, c) zbieżny, d) rozbieżny.