MATEMATYKA138

266 V. Całka oznaczona

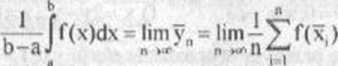
15. Jeśli funkcja f jest określona na przedziale < a,x) i całkowalna na każdym przedziale < a,P >, to wartością średnią funkcji f na przedziale < a,x) nazywa się liczbę y określoną wzorem

przy założeniu, że granica po prawej stronic istnieje. Obliczyć wartość średnią funkcji;

a)    y=e*/(2e* + l) dla 0<x<oo oraz dla !()()< x<oc.

b) y=cos²x, 0<x<qo.

Odpowiedzi.

!. a)2, b)0, c) jc/8, d) jc/2, e)ln2,    g) p^ln5’

h) X/3, i) 2(25^5-2)/l 5. j) rc/6, k) 2x^/9. 1 )x/4, ł)cosx-sinx, m) ln5

2.    a) 2/5, b) 2/3, c)jc/2-1, d) Iii2 2+x/2.

3.    a) 5/2. b) 2, c) 2-2/c, d)4, c) 16.

4.    a) 0, b)0, c) 1/2. d)0, c)0, 0 6.

5.    a), b), d) ujemny; c) dodatni.

6.    a)5/2£j£4, b) -SJ51, c) x/2sJse*/2

7.    a)9, b) 14/3, c) 1, d) I, c)*/Jl-\n2, 04/3.

8.    v₀T+aTV2.

9.    a) V2+x⁵ . b)-l/(x⁴fl), c)-l/(2(x²+l>^x), d) 2c ^4x‘-yo ^x5,/4

10.    a) nn przedziale (-2,2) funkcja rosnąca, na przedziale (2,6) funkcja malejąca, b) na przedziale (—3.0) funkcja wypukła, na przedziale (0.3) funkcja wklęsła

11.    o)2. b) 2/x, c) 1/2, d)x/2.

12.    Kb/4.

13.    v« v₀+^gT, g - wartość przyspieszenia ziemskiego 15. a) 1/2 dla obu przedziałów, b) 1/2.

3. CAŁKI NIEWŁAŚCIWE

b

Do tej pory przy omawianiu całki oznaczonej Jf(x)dx zakłada-

a

liśmy, żc przedział całkowania jest skończony i funkcja podcałkowa jest ograniczona na tym przedziale. Gdy b = +oo lub a - -oo lub funkcja

podcałkowa f jest nieograniczona, to symbolami

oo    b    oo

Jf(x)dx, Jf(x)dx, Jf(x)dx

a    -oo    -oo

oraz sy mbolem

J f(x)dx, gdy funkcja f jest nieograniczona

będziemy oznaczać nowy rodzaj całek - całki niewłaściwe. Rozpatrzy my całki niewłaściwe w przedziale niewłaściwym i całki niewłaściwe z funkcji nieograniczonej.

CAŁKI [NIEWŁAŚCIWE NA PRZEDZIALE NIEWŁAŚCIWYM. Niech f będzie funkcją określoną na przedziale <a,oo) i całkowalną na każdym skończonym przedziale <a,p >.

P

Granicę    lim |f(x)dx •

ft

nazywamy całką niewłaściwą funkcji f na przedziale niewłaściwym

w

a,oo) i oznaczamy symbolem Jf(x)dx. Zatem

(3.1)

jf(x)dx = lim Jf(x)dx

Przy tym. jeśli granica po prawej stronic (3.1) jest skończona, to mówimy,

oo

żc całka niewłaściwa Jf(x)dx jest zbieżna