MATEMATYKA132

254    V. Całka oznaczona

(2)    Funkcja całkowalna na przedziale domkniętym Jest także całkowalna na każdym podprzedziale domkniętym tego przedziału.

(3)    (addytywność względem funkcji podcałkowej). Jeżeli funkcje f i g są całkowalne na przedziale < a. b >. to również ich suma f ł g jest funkcją całkowalną na tym przedziale i przy tym

I)    b    b

J( f'(x)+g(x))dx-Jf(x)dx * Jg(x)dx

«    A    U

(4)    Jeśli [jest funkcją całkowalną na przedziale <a,b> oraz k - Const, to również funkcja kf jest całkowalna na tym przedziale i

b    h

Jkf(x)dx = kJf(x)dx

a    a

(5)    Zmiana wartości funkcji w skończonej liczbie punktów przedziału (nie wyklucza się przy tym końców przedziału) nie wpływa ani na całkowałność tej ftnkcji w tymi przedziale, ani na wartość całki, jeśli funkcja ta jest całkowalna.

(6)    (addytywność względem przedziału całkowania) Jeśli a.h.c są dowolnymi punktami przedziału, na którym funkcja f jest całkowalna, to

c    b    b

Jf(x)dx+Jf(x)dx=Jf(x)dx

a    c    a

(7)    Całka funkcji nieujemnej jest liczbą nie uje mną.

(8)    (monotoniczność całki oznaczonej) Jeśli funkcje f i g są całkowalne na przedziale < a, b > oraz f(x)£g(x) dla x e<a,b>. to również

b    b

Jf(x)dxśJg(x)dx

a    h

(9)    (dwustronne oszacowanie całki oznaczonej). Jeśli i jest funkcją całkowalną na przedziale <a,b > oraz mŚf(x)£M dla x €< a,b >. to

b

m(b-a)śj f(x)dxśM(b-a).

(10) Jeśli f jest fimkcją całkowalną na przedziale < a_s b >. to również funkcja |f|ye.s7 całkowalna na tym przedziale oraz

b    h

|Jf(x)dx|śJ|f(x)|dx

h    a

Natomiast z całkowalności funkcji |f| nic wynika calkowalność funkcji f (por. zadanie la i Ib w paragrafie I).

* o *

J=j’J ID.WDjfcO

a i 0

a 0 a    a

2lD₂|=2j

-a -a 0    0

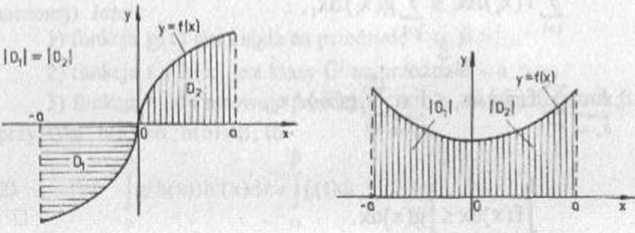
Rys 2.3

Rys 2.2

(11) a) Jeśli f jest fimkcją nieparzystą i całkowalną, to

n

J* f(x)dx = 0, (por. rys 2.2).

-o

b) Jeśli fjest funkcją parzystą i całkowalną, to a .    0    a

Jf(x)dx =2 jf(x)dx = 2jf(x)dx, (por rys 2.2).

-a    -a    0

Własność (11) wynika z interpretacji geometrycznej całki oznaczonej i własności (6). Pozostałe dowodzi się korzystając z definicji całki oznaczonej Z

Dowód własności (°) Prawdziwość tej własności wynika z następującego ciągu implikacji: