MATEMATYKA024

40 I. Wiadomości wstępne

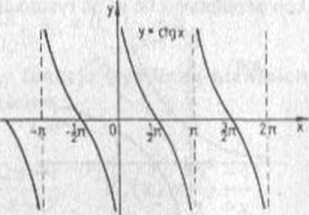
funkcją malejącą na każdym z przedziałów (k7C,(k + l)7i),gdzie k jest dowolną liczbą całkowitą (rys 3.1X).

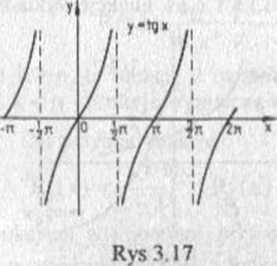
Rys 3.18

Funkcje y = tgx i y=ctgx są funkcjami okresowymi o okresie równym n. Funkcja y=cosx jest funkcją parzystą, a pozostałe funkcje trygonometryczne są funkcjami nieparzystymi.

FUNKCJE CYKLOMETRYCZNE Funkcja y = smx na przedziale <    > jest funkcją rosnącą, a więc różno wartościową. Istnieje

więc funkcja do niej odwrotna. Oznaczamy ją symbolem aresin Zatem y = sin x , x g<    y€C-l,l>

oraz

y = aresin x, x e<-1,1 >, y    >

są funkcjami do siebie odwrotnymi Funkcja sin przyporządkowuje

każdemu kątowi o mierze łukowej x €<-*,—•> wartość jego sinusa.

Natomiast funkcja aresin każdej liczbie xe<-l,l> przyporządkowuje k n

y £< -r_rT> takie, że sin y = x, czyli Z L

(y = aresin x) o (x = siny a ye<

Na przykład

aresin 0 = 0, gdyż «in0 = 0 i 0<=«r — — —■*

aresin(-1) = gdyż sin(-

1 n , _u .Ti 1 aresin- = gdyż sin - = -

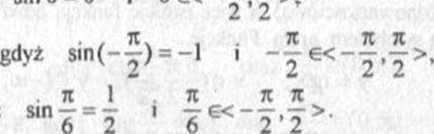
aresin —

Funkcja y = aresin x jest funkcją nieparzystą, to znaczy: aresin (-x) =-aresin x dla x €<-!,!>.

Wykres funkcji y = aresin x przedstawiony jest na rysunku 3.19

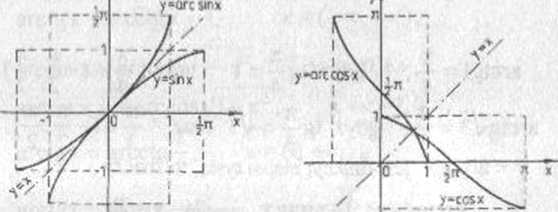
Rys 3.19

Rys 3.20

Funkcja y = cosx, xg<0,jc> jest funkcją malejącą, a więc równowartościową. Istnieje zatem funkcja odwrotna do niej i oznaczamy ją symbolem arccos. Tak więc, funkcje

y = cos, xe<0,7r>, ye<-l,l>

y = arccosx, xe<-l,l>, ye<0,7C> są funkcjami odwrotnymi do siebie, a ich wykresy' są symetryczne do siebie względem prostej y * x (rys 3.20), Z definicji ftinkcji odwrotnej mamy natychmiast, że

(y = arccosx) o (x = cosy a yc<0,7c>).

Na przykład

arccos 1 = 0, gdyż cosO =1 i 0 e< 0, k >,

arccos

1 n    n 1 k _A

arccos- = -, gdyż cos- = ~ i y€<0,7t>.