MATEMATYKA019

30 L Wiadomości wstępne

Zatem funkcje

f,(x) = l-x², xgR, oraz f₂(x) = l-x², xeR nie są funkcjami równymi, gdyż ich dziedziny są różne.

Określenie funkcji wymaga, na co wskazuje przytoczony wyżej przykład, określenia również dziedziny. Jeżeli funkcja jest określona wzorem

y = f(x)

i nic ma informacji o jej dziedzinie, przyjmujemy, że funkcja ta jest rozważana w tzw. dziedzinie naturalnej, czyli w zbiorze tych x, dla których wzór ma sens.

PRZYKŁAD 3.1 Wyznaczymy dziedzinę funkcji f, gdy:

a) f(x) = log(- +1) + ^4-|x-1|,

X

b) f(x) =

x

Iog(2x-x²)

a)    Dziedziną lej funkcji jest zbiór tych x e R, dla których 2

—+1>0 oraz 4-|x-l|>0.

Pierwsza z nierówności jest prawdziwa dla x €(-oo,-2)u(0,+oc)_f a druga - dla x €< -3,5 >. W konsekwencji dziedziną funkcji f jest zbiór D =< -3,-2)w(0,5>.

b)    Dziedziną funkcji f jest zbiór

D = {xeR: 2x-x²>0 a 2x-x^:*l} =

= {xeR: 0<x<2 a x?tl) = (0,l)u(l,2),    ■

WYKRES FUNKCJI Wykres funkcji f: D -> R, D c R jest to podzbiór W płaszczyzny R określony następująco:

W = {(x,y)eRⁱ: xeD a y = f(x)}.

PRZYKŁAD 3.2 Naszkicujemy wykresy funkcji: a) y = sin x+|sin x|, b)y=|x²-2x|. c) y = log(x-3). a) Rozpatrywaną funkcję zapisujemy w postaci:

y =

sin x + sinx, [sin x~sin x,

gdy sinx£0, gdy sin x < O,

czyli

{2sinx, gdy sin x £ O, O , gdy sinx<0. Wykres tej funkcji przedstawiony jesi na rysunku 3.1

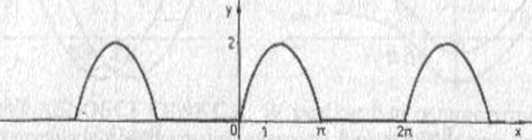
Rys 3.1

b) Funkcję zapisujemy w postaci:

{x²-2x, gdy x6(-®,0> u <2,+oo),

-x² + 2x, gdy x <=(0,2).

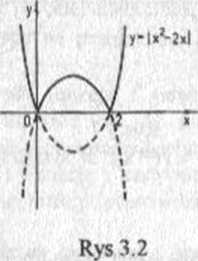
Sporządzenie wykresu danej funkcji sprowadza się do narysowania wykresów funkcji kwadratowych y = x^:-2x oraz y = -x^:+2x, a następnie wybrania właściwych części tych wykresów (rys 3.2).

Rys 3.3

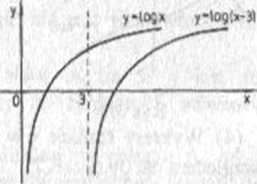
c) Najpierw szkicujemy wykres funkcji logarytmicznej y = logx a następnie przesuwamy go o wektor [3,0] (rys 3.3).    ■