MATEMATYKA013

18 I Wiadomoicl wstępne

18 I Wiadomoicl wstępne

i zapisujemy

Zatem

(2.7)

= Vw.

der

(z = %/w) o (zⁿ = w).

W szczególności, zgodnie z przyjętą tu definicją, pierwiastkiem stopnia drugiego liczby 4 jest 2 oraz -2, gdyż 2“' =4 oraz (-2)' =4.

Łatwo również widać, że v-9 = ±3i, gdyż (±3i)^: = -9.

TWIERDZENIE 2.4 Każda liczba zespolona postaci w -|w|(cos(p + isin <p) * 0 ma dokładnie n pierwiastków stopnia naturalnego n i są one dane wzorami:

m, q> + 2k7i . . (p + 2krc_v ,

=VN(cos—-— + isin—-—), k = 0,l,...,n-l,

(2.8)

gdzie ^w| oznacza arytmetyczny pierwiastek stopnia n modułu liczby w.

Szkic dowodu Niech Vw = z, przy czym z =|z|(cosO + i sin 0). Z definicji (2.7) mamy

|zT (cosn0 + isin n0) =|w|(cos(p + isin<p),

a stąd

1*1= s/M. e=---—”, k=o,±i.....

n

co oznacza, że pierwiastkiem n-tego stopnia liczby w jest każda liczba postaci

;_k =V^/N(

+ ism

COS-

n    n

Na koniec dowodzi się, że wśród tych nieskończenie wielu liczb z_v jest dokładnie n różnych między sobą, przy czym otrzymujemy je wstawiając n dowolnych, ale kolejnych liczb całkowitych na miejsce k, na przykład k = 0,1,..., n -1.    ' □

Uwaga 1 W zbiorze liczb zespolonych symbol a/w dla w * 0 i n » 2,3,... nie jest jednoznaczny , oznacza on dowolną spośród

<p ₊ 2krc._<p ₊ 2k*._{)ik = (Ul}.....

^zk =V-16, k = 0,1,2,3

n liczb określonych wzorem (2,8). Jedynie gdy w = 0, symbol len jest

lednoznaczny a/o = 0.

U w a g a 2. Zc wzoru (2 8) wynika, że pierwiaski slopnia n «> 2 liczby w są punktami płaszczyzny leżącymi na okręgu o środku w

l>oczątku układu i promieniu r =

= n/|wj,

przy czym dzielą ten okrąg na n

równych luków.

PRZYKŁAD 2.5 Rozwiążemy równania

a)z'+i = 0, b) z* +16 = 0, c) z⁵ - 5- 12i = 0.

Rozwiązanie każdego z tych równań jest równoważne obliczeniu pierwiastków odpowiedniego stopnia danej liczby.

a) Rozwiązaniami danego równania są liczby z_k = k = 0,1,2. Liczbę -i zapisujemy w postaci trygonometrycznej -i = l(cos(-7r/2) + isin(-7t/2)) i korzy stamy ze wzorów- (2.8):

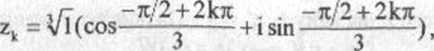
), k =0,1,2.

Stąd otrzymujemy

^zo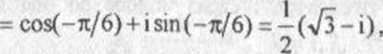

z, =cos(rc/2) + isin(7t/2) = i,

z₂ = cos(7 7r/6) + i sin(77t/6) = - cos(7t/6) - i sm(7t/6) =

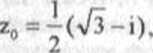
b) Rozwiązania tego równania to pierwiastki czwartego stopnia z liczby -16    _