MATEMATYKA020

32 I. Wiadomości wstępne

Przy sporządzaniu wykresów funkcji wykorzystujemy następujące informacje:

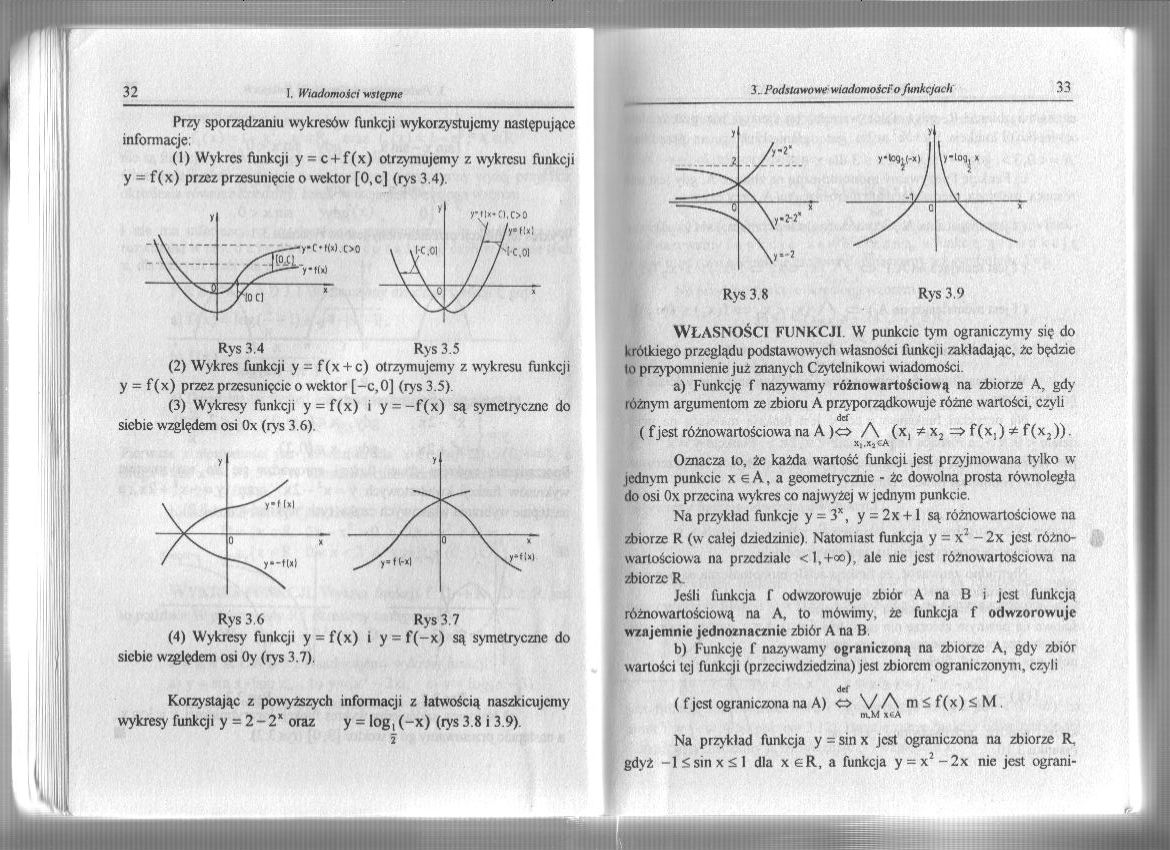
(1) Wykres funkcji y = c + f(x) otrzymujemy z wykresu funkcji y = f(x) przez przesunięcie o wektor [0,c] (rys 3.4).

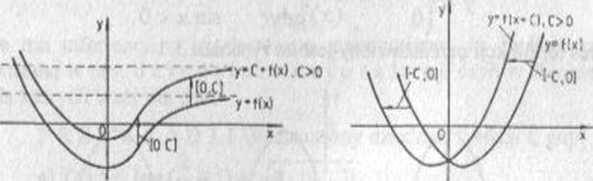
Rys 3.4    Rys 3.5

(2)    Wykres funkcji y - f(x + c) otrzymujemy z wykresu funkcji y = f(x) przez przesunięcie o wektor [-c,0] (rys 3.5).

(3)    Wykresy funkcji y = f(x) i y = -f(x) są symetryczne do siebie względem osi 0x (rys 3.6).

Rys 3.6    Rys 3.7

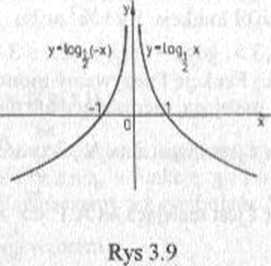
(4) Wykresy funkcji y = f(x) i y = f(-x) są symetryczne do siebie względem osi Oy (rys 3.7).

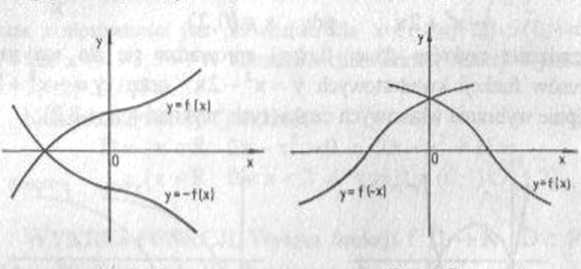
Korzystając z powyższych informacji z łatwością naszkicujemy wykresy funkcji y = 2-2^x oraz y = log,(-x) (rys 3.8 i 3.9).

WŁASNOŚCI FUNKCJI W punkcie tym Ograniczymy się do krótkiego przeglądu podstawowych własności funkcji zakładając, że będzie to przypomnienie już znanych Czytelnikowi wiadomości.

a)    Funkcję f nazywamy różnowartościową na zbiorze A, gdy różnym argumentom ze zbioru A przyporządkowuje różne wartości, czyli

def

( f jest różnowartościową na A )o A (x, * x₂ f(x,) * f(x₂)).

X|.Xj€A

Oznacza to, żc każda wartość funkcji jest przyjmowana tylko w icdnym punkcie xeA,a geometrycznie - żc dowolna prosta równoległa do osi 0x przecina wykres co najwyżej w jednym punkcie.

Na przykład funkcje y = 3^X, y = 2x + l są różnowartościowc na zbiorze R (w całej dziedzinie). Natomiast funkcja y = x‘ -2x jest równowartościowa na przedziale <1,+oo), ale nic jest różnowartościową na zbiorze R

Jeśli funkcja f odwzorowuje zbiór A na B i jest funkcją różnowartościową na A, to mówimy, że funkcja f odwzorowuje wzajemnie jednoznacznie zbiór A na B.

b)    f unkcję f nazy wamy ograniczoną na zbiorze A, gdy zbiór wartości tej funkcji (przcciwdzicdzina) jest zbiorem ograniczonym, czyli

dtf '

( f jest ograniczona na A) o V A m ś f(x) <, M.

m.M x* A

Na przykład funkcja y = sin x jest ograniczona na zbiorze R. gdyż -1 <:sin x £ I dla xeR, a funkcja y = x^: -2x nie jest ograni-