MATEMATYKA023

I. Wiadomości wstępne

FUNKCJE WYMIERNE. Funkcja wymierna jest to iloraz dwóch wielomianów:

R(x) =

i    ^    ^0 * ^ *

Jeżeli k 't n, to funkcję R nazywamy funkcją wymierną niewłaściwą; jeżeli k < n - funkcją wymierną właściwą.

Na przykład funkcje

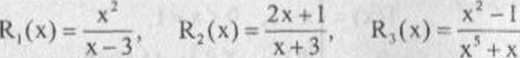
są funkcjami wymiernymi, przy czym R, i R_; są funkcjami wymiernymi niewłaściwymi, a R, - funkcją wymienią właściwą.

Każdą funkcję wymierną niew łaściwą można przedstawić jako sumą wielomianu i funkcji wymiernej właściwe], a uzyskujemy to dzieląc licznik przez mianownik.

Funkcje wymierne gdzie n e N. zaś a, A. B, p. q są dowolnymi współczynnikami rzeczyw istym, nazywamy ułamkami prostymi odpowiednio I i II typu.

Każdą funkcją wymierną właściwą można przedstawić w postaci sumy skończonej liczby ułamków prostych.

Uatwo na przykład sprawdzić, że

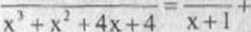
x² +4

x + 6    1

2 - x

dla każdego x z dziedziny tej funkcji.

Bez odpowiedzi na razie pozostawiamy pytanie, w jaki sposób, mając daną funkcję wymierną znajdujemy ułamki proste, których sumą jest ta funkcja. Do tej sprawy wrócimy jeszcze w- tym paragrafie, po omówieniu funkcji elementarnych.

FUNKCJE WYKŁADNICZE 1 LOGARYTMICZNE. Funkcja wykładnicza y = a* i funkcja logarytmiczna y = log, x, 0 < a * 1 są funkcjami odwrotnymi do siebie. Dziedziną dowolnej funkcji

3. Podstawowe wiadomości o funkcjach

39

wykładniczej jest zbiór R, a przcciwdziedziną R₊. Dziedziną funkcji logarytmicznej jest zbiór R,. a przeciwdziedziną zbiór R. Wykresy tych funkcji przedstawione są na rysunkach 3.13 i 3.14. Funkcje wykładnicze

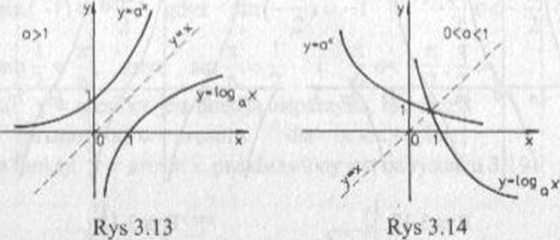
i logarytmiczne są funkcjami rosnącymi, gdy a >1, a malejącymi, gdy 0<a < 1.

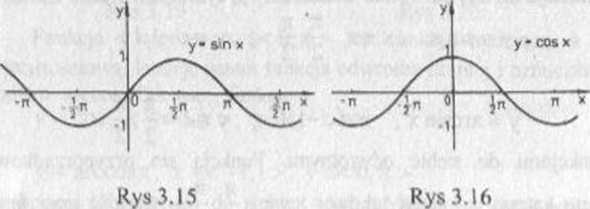
FU.NKCJE TRYGONOMETRYCZNE. Funkcje trygonometryczne sinus i cosinus są określone dla każdego x eR, a ich przeciwdziedziną jest przedział < —1,1 >. Funkcje y=sinx i y=cosx są przedziałami monotonicznc i okresowe o okresie podstawowym 271. Wykresy tych funkcji przedstawione zostały na rysunkach 3.15 i 3.16.

Funkcja y tgx jest określona dla x * ~ +■ k:t i jest rosnąca na

każdym z przedziałów (-y+kjt,-~+kji), gdzie k jest dowolną liczbą całkowitą (rys 3.17). Funkcja y -ctgx jest określona dla x * kn i jest