132(1)

-i run*i|«--

4.7. FUNKCJA WYMIERNA y = §

4.7.1. Definicja funkcji wymiernej

Funkcja wymierna to iloraz dwóch wielomianów jednej zmiennej

'M-Wr ^Q{x)*°- S

Dziedziną funkcji wymiernej jest zhiór liczb rzeczywistych bez miejsc zerowych widomi' n nt nowniku

^D, = *\{*"• Q(^x) ^a °}»oyli    = {x e R:Q(x)i: o}.

_{/W =} _3^Li

,v*- 4.v + 3 _ Ir - 1

4.7.2. Przykłady funkcji wymiernych

4. FUNKCJE

CD

^/W'7-4*+7    __

f(x) = £,a*0-.    D,= R\{ 0}

(proporcjonalność odwrotna)

Funkcja o wzorze y = — (a £ 0) jest szczególnym przypadkiem funkcji wymiernej. Dziedziną tej: jest: D, = /f\{0}.

D_f- R

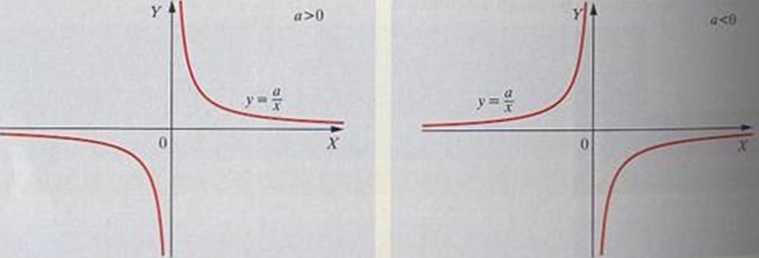
Uwaga: Przesuwając wykres funkcji y = ^ wzdłuż osi układu współrzędnych, otrzymujemy wykresy pujących funkcji:

y = Y*-"p (P° przesunięciu wzdłuż osi OX - por. 4.2.) lub

y = Y + (j (po przesunięciu wzdłuż osi OY - por. 4.2.) lub

y = -y - j; ⁺ <I (po przesunięciu wzdłuż obu osi układu współrzędnych - por. 4.2.)

4.8. FUNKCJA WYKŁADNICZA

4.8.1. Definicja funkcji wykładniczej

Funkcja wykładnicza (argument w wykładniku) to funkcja postaci

y = </'.</> 0, x € R.    „—

Uwaga: Dla a = 1 funkcja wykładnicza >• = «'- I staje się funkcją liniową (stałą), stąd tez ^ na przyjąć dodatkowo, że a ^ 1.

Dziedzina funkcji wykładniczej: f) . R.

4.8.2. Własności funkcji wykładniczej

[₍„<₀<')-|(^^a')^Nl^(fn,ale<^ąca)

_{) „O-[(•'•= ^,)l<^{r s,a,,>}

f , \ V = </' (jest równowartościowa)

■ _t> 0 (funkcja przyjmuje wartości dodatnie dla każdego .v e D_f)

₀brak miejsc zerowych gjbrak ekstremum

h) punkt szczególny: r = (0; I)

4.8.3. Wykres funkcji wykładniczej

Wjlats funkcji wykładniczej to krzywa wykładnicza - jej położenie zależy od wartości podstawy u (>0).

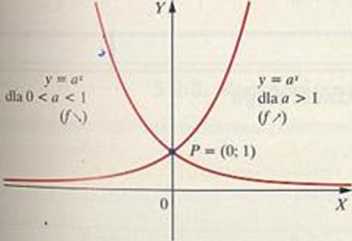
dla (a >()i<i/l)

Y	> = >
	/> = (0:1)
0	X

dlau - I mamy y ■ 1‘ « 1

4. FUNKCJE

C^L

CD

k*³*^23- Wykresy funkcji: y = a i y = | -Jj j są do siebie symetryczne względem osi OK (a € (I: +oo)« -jj G (0:1) j.