50 (151)

3.1. FUNKCJA LINIOWA

3.1.1. Definicią, wykres i własności funkcji liniowej

Funkcja liniowa to funkcja postaci:

/. .v — y = ax + b\ a, b e R (ustalone)

D = R, D~^x = R, a - współczynnik kierunkowy, h — wyraz wolny.

Wykresem funkcji liniowej jest prosta nachylona do pólosi OX* pod kątem a, takim, że a = tg 0f, i przecinająca oś OY w punkcie (0; b):

,a = 0

d) dla ł — brak miejsc zerowych: b 0

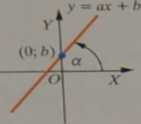
yt
(0; 6)1	•O II >%
	b > 0
O	X

(0;6)T

b < 0 y-b

Własności funkcji liniowej: a) / s\ a > 0    / stała: a — 0

/ v. a < 0

e) dla 1 °    ° : y = ax - proporcjonalność prosta

I b = 0

Uwaga: Na płaszczyźnie z układem współrzędnych XOY równanie: y = ax + b przedstawia prostą.

<

Natomiast każdej z nierówności: y ax ⁺ b bib

y    + b odpowiada półpłaszczyzna pod lub

nad prostą o równaniu y = ax + b na przykład:

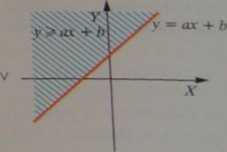
zaznaczone pólpłaszczyzny wraz z prostą, gdy nierówność jest słaba, nieostra (^,

Y	y = o
O	X

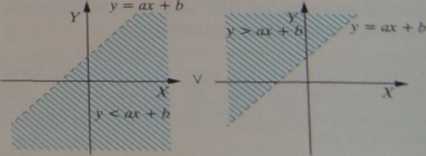
zaznaczone pótptaszczyzny bez prostej, gdy nierówność jest ostra, mocna (<, >)

3.1.2. Równania i nierówności liniowe z wartością bezwzględną

Por. 1.6.1. i 1.6.2.