CCF20090319041

50

Różniczkowanie funkcji

Oznaczenie pochodnej w symbolach różniczkowych

dy_ _ df(x) dx dx

/'(*)

wynika ze wzoru (2.24). Jeśli umiemy liczyć pochodne, to znajdowanie różniczek nie powinno sprawiać żadnych kłopotów. Obliczmy przykładowo różniczkę funkcji y — x² — 3x + 1 dla x = 4. Pochodna tej funkcji y' = 2x — 3, a więc różniczka wyraża się wzorem

dy = (2x — 3 )dx.

Weźmy dx = 0,1 jako różniczkę zmiennej niezależnej. Różniczka funkcji jest równa dy = (2 • 4 — 3) • 0,1 = 0,5, natomiast przyrost funkcji Ay w tym punkcie wynosi 0,51.

Obliczmy różniczkę funkcji y będącej sumą lub różnicą dwóch funkcji y(x) = u(x) + v(x). Wówczas

dy — (u' + v')dx = u'dx -f v'dx — du-f- dv,

zatem

d(u ±v) = du± dv.    (2.25)

Podobnie można wykazać, że różniczki iloczynu i ilorazu funkcji wyrażają się wzorami

d(uv) = v du -f u dv,

(2.26)

Różniczka funkcji zm stępujące we wzorze błędem. Błąd wieli :e rzystając z różniczki-

Wykażemy to na prz pomocą wahadła cia nego o długości l wyi

1

Różniczkę funkcji g l

Jeżeli maksymalny : długości l, oznaczym okresu drgań przez

oznacza maksymalny w tym doświadczeni:

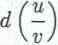
v du — udu

(2.27)

i wstawieniu do wzc:

Jeżeli / jest funkcją dwóch zmiennych f(x,y) określoną w punkcie P(x₀, y₀) i różniczkowalną w tym punkcie, to różniczka funkcji / w punkcie P ma postać

Iloczyny

w_ix w.

dx ’ dy^V'

gdzie dx i dy oznaczają dowolne przyrosty zmiennych niezależnych, a pochodne są policzone w punkcie P, nazywamy różniczkami cząstkowymi funkcji f(x,y) w P.

Można obliczyć błąd przez g = 47r²l/T²z

Widać, że duży vcp skiego ma dokładne odmierzyć czas jak ]

Jak się wkrótce pr; całkowym.