273 (9)

monotoniczność zależy od a

10.3.2. Definicfa, wykres i własności funkcji logarytmicznej

,_|tKja logarytmiczna (argument pod logarytmem) to funkcja postaci: log, .tło > 0 A <ł 1, X e R_t. pnedzina fankąji logarytmicznej: D_{l0fa t}= R_t •Htisnoici Itanktji logarytmicznej:

,l)(o| 1) - {()’ = >°g₀*) '] (f- rosnąca) jt)(0<«< 0 *= [(>’= log_a^) N.J (f- malejąca)

IWIlB ^r^ⁿowartościowa (P^or- uwaga 1 w 10.2.1.) j| A log, x e rt(f. przyjmuje wartości rzeczywiste)

| ma jedno miejsce zerowe x₀ = I lO brak ekstremum

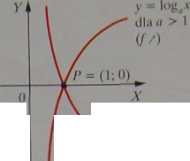
mPunkt szczególny P = (1; 0) (por. w 10.2.1c.)

jigjktra funkcji logarytmicznej to krzywa logarytmiczna - jej położenie zależy od wartości a |_tf>0Aa# 1)

Uwaga 1: Wykresy funkcji y = log₀x i y = log|xjx są do siebie syme-

inone względem osi OX (por. uwaga 2 w 10.2.1.).

Ungb 2: Wykres funkcji logarytmicznej ma w r = 0 prawostronną sąmplotę pionową: x = 0 (oś OY- por. 11.1.1.).

+00 dla a 6 (0; l)    >■ = iog„.t

-oo dla ae(l;+oo)    \ dla0 <a < 1

( Własnośćfunkcji logarytmicznej: y = log_ax(a > 0 A a i= l) wynikająca z różnowartościowości i stosowa-udo rozwiązywania równań logarytmicznych (por. 10.2.1e.):

(log,^ log„x₂) « (x, = x₂j

(logarytm o podstawie a można opuścić)

‘Własność funkcji logarytmicznej: y = log_ax (a>0An/ l) wynikająca z monotoniczności i stosowana fcniniązywania nierówności logarytmicznych (por. 10.2.1f.):

dla 0 < I < 1		dla a > 1
toS.*! log. *2	logax,> logax2	11*! I°8j *2	logax,< logax2
1	1	8	i
X,>X,	_w ~A	*t> *2	x,<x2
£ (0; 1) wartości funkcji/(x,) = logax,		Dlaa e (1; +oo)wartości funkcji/(x,) = logax,
'/I^1,) = log,x2 są w odwrotnej zależności, jak		i f(x2) = logax, są w takiej samej zależności, jak
argumenty x, i xY		argumenty x, i x2.

'^Zależności w powyższej tabeli odnoszą się również do nierówności słabych.

(Biedronia

i?¹⁰ linia krzywa przestrzenna („ukośnobież-poprowadzona na kuli i przecinająca wszyst-Prudniki pod statym katem (różnym od pro-

k

dalekobieżnych oraz samolotów ”*^lrzu lecących prosto „przed siebie” mają

10. FUNKCJE POTĘGOWE, WYKŁADNICZE I LOGARYTMICZNE

tabg₁x=

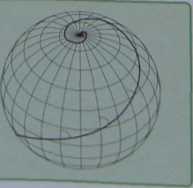
postać zbliżoną do lok-sodromy.

Nazwa „loksodro-ma” została wprowadzona w 1624 roku przez uczonego holenderskiego Snclliusa.