MATEMATYKA134

258 V Całka oznaczona

Stosujemy podstawienie arccos2x = t Wówczas

₇‘ dx = -ldl.

Vl~4x‘

Ustalamy następnie granice a i P dla nowej zmiennej t: jeśli x = 0, to t = arccosO = 7t/2, gdy x = 1/2, to t = arccosl = 0. Ostatnie "przeliczenia" można zapisywać krócej w tabeli:

X	0	1/2
t	*/2	0

Otrzymujemy więc

£

48

1/2

[ (arccos2x)‘ I Vl-4X²

TWIERDZENIE 2.3 (o całkowaniu przez części dla całki oznaczonej). Jeżeli funkcje fi g są klasy C¹ na przedziale < a,b >, to b    h

(2.3)    J f(x)g'(x)dx = f(x)g(x)|_a^b - J f'(x)g(x)dx.

a    a

PRZYKŁAD 2.4 Obliczymy całkę:

JVcos2xdx

= -x²sin2x +Jxsin2xdx =

f(x)*x², g'(x)-cos2x

f'(x)s2x, g(x)»-*in2x 2

n    1    * j *    11*

-1 xsin2xdx =...**-xcos2x —fcos2xdx = -n—sin2x =-tc {    ²    o    2    4 l 2

FUNKCJA GÓRNEJ GRANICY CAŁKOWANIA Niech f będzie funkcją całkowalną na przedziale <a,b>. Dla każdego x €< a, b > rozważamy całkę

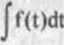
x o

Całka ta istnieje, gdyż f jest funkcją całkowalną na przedziale <a,b > i przedział <a,x> jest podprzcdaałem przedziału <a,b>. Jeśli x jest ustalone, to całka ta jest określoną liczbą Potraktujmy teraz górną granicę x jako zmienną z przedziału < a,b >; wówczas całka ta będzie funkcją tej zmiennej - funkcją górnej granicy całkowania, Oznaczmy ją literą F:

F(x) = Jf(t)dl, xe<a,b>.

Interpretacja geometryczna funkcji F przy założeniu, źc f(x) £ 0, jest podana na rysunku 2 4

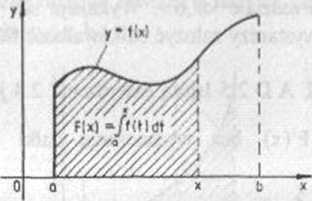
Rys 2.4

Można oczekiwać, że własności funkcji F takie, jak ciągłość, różniczkowalność są zależne od własności funkcji podcałkowej f. Jest tak istotnie. Traktuje o tym następujące

TWIERDZENIE 2.4 (o pochodnej funkcji górnej granicy całkowania). Jeżeli f jest funkcją ciągłą na przedziale < a,b >, to funkcja x

F(x) = J f(t)dt jest różniczkowalna na tym przedziale i przy tym n

x

(2.4)    F'(x)=^t(Jf(l)dt) = f(x), xe<a,b>.

»

D o vi.ó d Niech d> oznacza dowolnie ustaloną funkcję pierwotną funkcji f (jej istnienie wynika z ciągłości funkcji 0 Zatem, zgodnie z wzorem Newtona- Leibniza, mamy

F(x) = 0(x)-i(a) dla xeca.b>.