MATEMATYKA149

288 V. Całka oznaczona

PRZYKŁAD 4.6 Obliczymy pole figur ograniczonych liniami:

a)    parabolą y = -x^: +2x-2 i prostymi y = x+1, x = - l,x = 2,

b)    parabolami: x = 2y-y² i x = y² -4,

c)    hiperbolą y=2/x dla x>0 i prostymi y=x + 1,y=x-l, x=0.

a) Ponieważ D=((x,y)eR^;;-l£x£2,-x²+2x-2śyśx + l}

(por. rys 4 10), więc zgodnie z (4.5) mamy:

r    ²

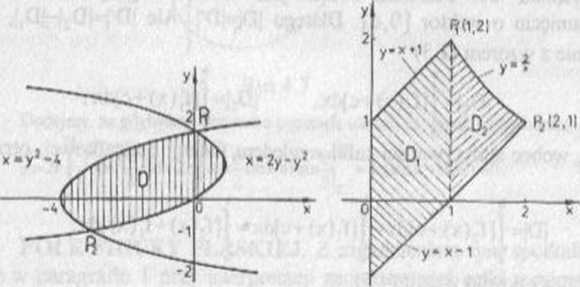
|D|= J[(x + l)-(-x’ + 2x-2)]dx = J(x³-x + 3)dx = 2l/2.

Rys 4.11

Rys 4 12

b) Parabole przecinają się w punktach P, (0,2) i P₂(-3, 1), (rys 4 11). Ponieważ D={(x,y)€=R* y‘-4sxS2y-y²,-lśy^2}, więc

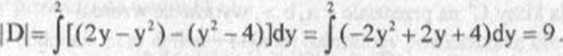
•i    i

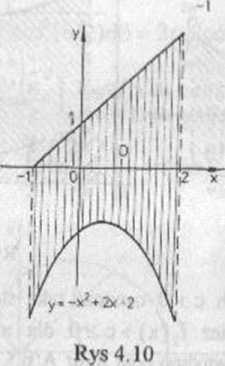
c) Znajdujemy najpierw punkty przecięcia P,(l,2) i P_?(2,1). Górna linia ograniczająca figurę D, (rys 4.12), składa się z dwóch linii: y = x ♦ 1 oraz y •= 2/x. Dlatego figurę tę prostą x = I dzielimy na dwie figury' D, i D₂, gdzie D, jest rówmoległobokicm o polu |D,|=2, natomiast D₂s={(x,y)€R²: l<x£2, x-l<y£2/x), ajej pole

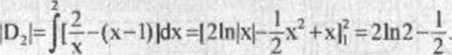
Ostatecznie otrzymujemy |D|=|D,|+jD₂(=l_ł5+2ln2.

Objętość bryły obrotowej, pole powierzchni OBROTOWEJ

TWIERDZENIE 4.5 Objętość |V| bryły V, (rys 4.13), powstałej w wyniku obrotu dokoła osi 0x trapezu krzywoliniowego D={(x,y)eR²: a<x£b, 0£y£f(x)}, gdzie f jest funkcją ciągłą na przedziale <a,b>, wyraża się wzorem:

h

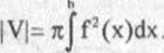
(4.6)

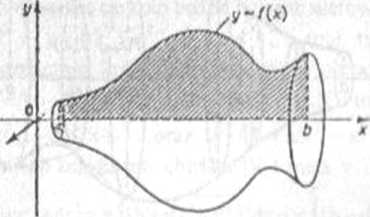
Rys 4.13