31 (584)

liczby przez wszystkie liczby od 2 do o jeden od siebie mniejszej. Aby wiedzieć, czy znaleźliśmy podzielnik, czy nie (a przy okazji nie sprawdzać podzielności po jego znalezieniu), wykorzystujemy zmienną logiczną Pierwsza. Ma ona wartość True, kiedy uważamy, że liczba jeszcze może być pierwsza, False, kiedy już mamy pewność, że nie.

Pomimo tego, że gdy już znajdziemy podzielnik, nie sprawdzamy dalej podzielności, pętla musi jednak wykonać kolejne jałowe obiegi (aż I osiągnie wartość N-l). Aby temu zapobiec, możemy zastosować dwie metody: zastosować inny rodzaj pętli, opisany w kolejnym rozdziale lub użyć instrukcji break, która powoduje bezwarunkowe wyjście z pętli (zarówno for, jak i opisanych w następnym podrozdziale) i przejście do pierwszej instrukcji za pętlą. Odpowiedni fragment programu mógłby mieć postać:

if Pierwsza then

if (N mod I-O) then begin

Pierwsza False;

Break;

end;

Nie jestem zwolennikiem używania tej metody, która według mnie zaburza nieco strukturalność (sam zapewne użyłbym po prostu innego rodzaju pętli), tym niemniej uważam, że trzeba się z nią zapoznać i nie jest grzechem jej roztropne używanie.

W ćwiczeniach dodatkowych będziesz miał możliwość poprawienia programu zgodnie ze spostrzeżeniami z ćwiczenia 1.10 i sprawdzenia, czy daje to znaczne skrócenie czasu pracy.

Schemat pętli for

Narysuj schemat blokowy instrukcji for I := Początek to Koniec do {blok instrukcji}.

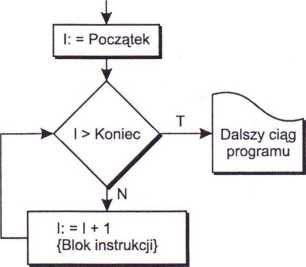
Powyższy schemat często podawany jest teoretycznie, jednak gdyby został wykorzystani przez kompilator Turbo Pascala, to niemożliwa byłaby następująca sekwencja instrukcji:

var

I : Byte; begin

for I := 0 to 255 do {instrukcje}