328 (9)

m\ =//i₍f[F-TP~^!F, -fXP”^lB⁷ (BP^_1B^T)^-i BP'"ⁱF'₎) = 0.00040 (.„)² flZ2    “    “

m,-,    — 0.020 (m)

“7-2

Przykład 5.2.2

Stosując metodę warunkową, wyrównać sieć niwelacyjną z przykładu 5.1.1. Obliczyć błąd średni wyrównanego przewyższenia h_Ą oraz błąd średni wyrównanej wysokości punktu Z₃.

Rozwiązanie

Również i ta sieć (przez repery R_v R^), jest dowiązana do układu współrzędnych (układu wysokości II), stąd d, - 0. Nie zawiera również defektu wewnętrznego, czyli d_w - 0. Zatem d = </, r d_w ~ 0. Ponadto, skoro n - 5 i r ~ 2, to/- n -r i- d ~ 2. Jedno z dwu wymaganych równań warunkowych, podobnie jak w poprzednim przykładzie, można utworzyć korzystając z warunku „zamknięcia oczka niwelacyjnego” (rys. 5.2.5)

hn - h.\ +1‘5 — 0

Natomiast drugie równanie może wynikać z „przejścia od reperu do reperu”, przy czym dostępne są tutaj dwie drogi. Wybierając jedną z nich (rys. 5.2.5), zapiszemy

h\ + h₂ - ^3 + H - // k₂ ~ 0

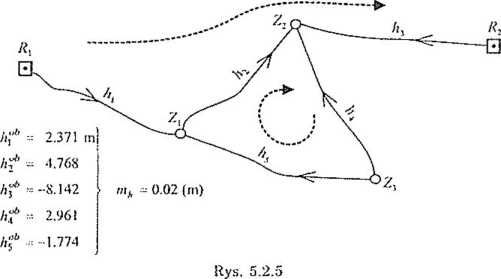
Możliwy do przyjęcia jest także inny zestaw dwu równań, np. dwa „przejścia od reperu do reperu” (ale już bez „zamknięcia oczka”, które jest kombinacją tych „przejść”). Wybierając wcześniej ustalony układ równań warunkowych

Il-y -- /l.j + /l<| — O /_l|+/r₂-/_l3+//^_|-//_%=0j

oraz podstawiając h_t - hf^J + v,_:, bezpośrednio uzyskujemy

hf+v₂~(hf -rv,)4-/if f v₅ - 0 '    |

h\^,b + v, + hf + v₂ - (/«f + v₃) + //_A, - H ,_{2 oj

v2	► . t ^{,b 1 1. n *• Vą + "f ho —łiĄ *ł* h^ —u S ■ -----V-
	ii] =--0.022 {111)
V| -i- \>2 -v3	■f hf+hf-hf + hR[
	A ) =0.033 (ni)

Na podstawie układu (*) zestawiamy macierze

B =	"0 1	0 -i l]	A =	'-0.022
	l 1	"1 0 »J		0.033

Wspólna wartość błędu średniego pomiaru wszystkich przewyższeń pozwala na zapisanie macierzy wag w postaci P = wijj" I3, a stąd P“^[=m_AI ₅. Kontynuując obliczenia, wyznaczamy

bp~'b⁷'

0.0012	0.0004‘		. T , 937.5 (BP 'B^1 ) ‘ =	-312.5]
(1.0004	0.0012	(m>^2	-312.5	937.5j(

a następnie:

Wektor korelat i wektor poprawek

0.012

K = -(BP"^,B^rr^lA =

30.9

37.8

(m)‘

-0.003

-0.012

0.015

-0.015

J(ui)

Warto zwrócić uwagę, że uzyskane wartości poprawek są takie same jak w przykładzie 5.1.1 ( ta sama sieć wyrównana metodą parametryczną)-

329