335 (36)

(Hf — pole magnetyczne w ferromagnetyku). Znajdujemy zatem

H₀ = H + iV(_iu-l)H_/.    (86.7)

Z drugiej strony, jeśli weźmiemy pod uwagę element powierzchni wnęki prostopadły do kierunku pola, a więc taki, że przy przejściu przezeń kierunek pola nie ulega zmianie i zastosujemy znane nam już warunki graniczne, to otrzymamy

B₀ = B_f    (86.8)

(w tym przypadku składowa normalna wektora indukcji magnetycznej równa jest samemu wektorowi). Mamy zatem

l*o H₀ = [Xfi₀ Hf,    (86.9)

skąd

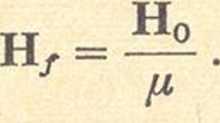
(86.10)

Podstawiając tę wartość do wyrażenia na H₀, znajdujemy ostatecznie

NQt-1)

H₀ = H +

H

(86.11)

skąd

H₀ =

juH

[x-N(n~ 1)

(86.12)

Liczba N jest zawsze ułamkiem właściwym. Wartości jej podawaliśmy już poprzednio, omawiając właściwości dielektryków (por. § 19). Dla ciała w kształcie płaskiej płytki o małej grubości N = 1, dla ciała w kształcie długiego walca o małej średnicy N = 0, dla kuli N — |.

Jeżeli w ciele ferromagnetycznym wytniemy wnękę w kształcie wąskiej szczeliny poprzecznej względem kierunku pola magnetycznego, to znajdujemy dla niej

H₀ =,

= /zH.

wH^!

(86.13)

Jeśli natomiast wytniemy wnękę w kształcie długiego walca o osi równoległej do kierunku pola magnetycznego, znajdziemy

(86.14)

H₀ = ^-=H.

Z zestawienia dwu tych pomiarów możemy znaleźć /jl. Określając natężenie pola magnetycznego w ciele ferromagnetycznym należy zawsze pamiętać o omówionym tu wpływie kształtu ciała.

87. Histereza magnetyczna

Pomiary wykazują, że dla ciał ferromagnetycznych związek pomiędzy namagneso' waniem H_f a natężeniem pola H jest bardziej skomplikowany niż w ciałach dia- i para' magnetycznych. Występuje tu mianowicie charakterystyczne zjawisko histerezy magne^

335