34 (423)

Optyka

322. Rysunek 88 przedstawia przejście promieni przez siatkę dyfrakcyjną (proporcje nie są zachowane).

Optyka

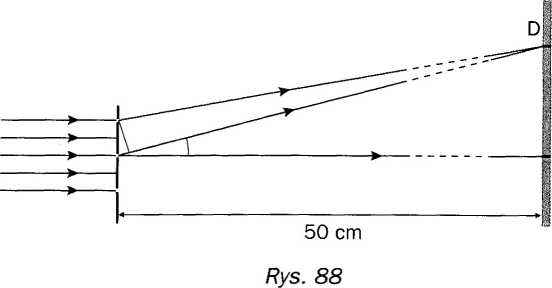
a.    Oblicz sinus kąta między kierunkiem pierwotnym wiązki i promieniem, który w wyniku interferencji daje prążek I rzędu.

b.    Oblicz długość fali światła padającego na tę siatkę dyfrakcyjną, jeśli odległość między szczelinami a= 2,5/im.

©dbicie, lataniami© i rozproszenie światła

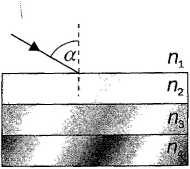
Rys. 89

Promień świetlny pada pod kątem 60° na układ trzech płytek z różnych substancji (rys. 89). Narysuj przybliżony bieg promienia, jeżeli współczynniki załamania tych substancji są odpowiednio równe: n₁ = 1, n₂ = 1,44, n₃ = 1,33 i n_Ą = 1,66.

Z jaką szybkością porusza się światło w wodzie o współczynniku załamania n_w = 1,33, jeśli w powietrzu (n_p = 1) jego szybkość jest równa 3 • 10⁸ m/s?

32 So Oszacuj, pod jakim kątem do normalnej załamie się promień świetlny przechodzący z wody o współczynniku załamania n_w = 1,33 do szkła o współczynniku załamania n_s = 1,5, jeśli kąt padania wynosi a = 60°.

Kasia nurkując w jeziorze, widzi Słońce pod kątem 30° do normalnej. Oszacuj kąt, jaki tworzy promień słoneczny z lustrem wody. Przyjmij współczynnik załamania wody względem powietrza n_w = 1,33.

i_____

327.    Współczynnik załamania wody w basenie wynosi n_w = 1,33. Jaki głęboki jest w rzeczywistości basen, jeżeli Ela stojąc na brzegu, szacuje jego głębokość na 150 cm.

Wskazówka: W prawie załamania, ze względu na małe kąty, sinusy kątów możemy zamienić na ich tangensy.

328.    Oblicz kąt graniczny dla:

a.    płytki o współczynniku załamania n₁ = 1,5,

b.    wody o współczynniku załamania n_w = 1,33,

c.    diamentu o współczynniku załamania n_a = 2,4.

Podaj ogólny wzór na kąt graniczny w przypadku załamania światła na granicy substancji o współczynniku załamania n_s i powietrza.

\

329.    Na rysunku 90 narysuj dalszy bieg promienia świetlnego padającego na pryzmat o współczynniku załamania n_p = 1,5.

Rys. 90

,13@o Na rysunkach 91 a i b wiązka światła białego pada na pryzmat. Jaki obraz otrzymamy na ekranie w sytuacji przedstawionej na rysunku 91 a, a jaki w sytuacji na rysunku 91 b?

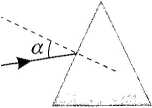
a.

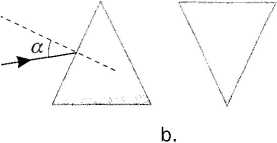
Rys. 91

P@wstawani® ©ts>mz@w w zw@@re§adl&adhi

i § 13 o Korzystając z prawa odbicia, wykonaj rysunek, a następnie oblicz wysokość lustra, jakie powinna kupić Grażyna, aby mogła się w nim cała przeglądać. Grażyna ma 165 cm wzrostu, odległość między jej oczami i czubkiem głowy przyjmij 10 cm.